Sorting Algorithm Introduction - 排序算法简介

Made by Mike_Zhang

---

数据结构与算法主题：

---

1 Introduction to Sorting Algorithm

Sorting is a process of arranging a sequence of elements into some logical order (e.g. increasing or decreasing order).

Nowadays, most of programming languages and computer systems have implementations of sorting algorithms.

But, it is still very important to know and study how to implement sorting algorithms as

1. Sorting algorithm can be used to solve other problems in a similar way;
2. Sorting algorithm can be the first step of solving other problems;
3. Sorting algorithm analysis is a good practice of algorithm performance analysis.

Let’s introduce some popular sorting algorithms: Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort, Counting Sort, Heap Sort, etc.

(Assume all resulting arrays are sorted in ascending order.)

---

2 Bubble Sort

冒泡排序

Algorithm:

1. Starting from the first element, compare the first adjacent elements of the array, if the first element is larger than the second element, swap the two elements;
2. Repeat doing step 1 for each pair of adjacent elements from the first element to the last element, end up with the biggest element in the last position.
3. Repeat doing above steps for all element except the last element;
4. Each time, the relatively biggest element will be moved towards the end of the array, the array is sorted when no swap is made.

Illustration:

Source: VisuAlgo

Java implementation:

public static void bubbleSort(int[] inArr) {
    int n = inArr.length;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (inArr[j] > inArr[j + 1]) {
                int temp = inArr[j];
                inArr[j] = inArr[j + 1];
                inArr[j + 1] = temp;
            }
        }
    }
}

Test:

public static void main(String[] args) {
        int[] arr = {29, 24, 20, 37, 14};
        bubbleSort(arr);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
}

14 20 24 29 37 

Average time complexity: $O(n^2)$
Worst time complexity: $O(n^2)$

---

3 Selection Sort

选择排序

1. Starting from the first element, find the smallest element in the array, swap it with the first element;
2. Then find the next smallest element in the array, swap it with the second element;
3. Repeat in the above way until the array is sorted.

   Each time we select the smallest element in remaining unsorted array, and move it to the beginning of the unsorted part of array (or end of sorted part).

Illustration:

Source: VisuAlgo

Java implementation:

public static void selectionSort(int[] inArr) {
    int n = inArr.length;
    for (int i = 0; i < n; i++) {
        int minEle = i; // Default smallest element is the first element
        // Find the smallest element iteratively
        for (int j = i + 1; j < n; j++) { 
            if (inArr[j] < inArr[minEle]) {
                minEle = j;
            }
        }
        // Swap the smallest element with the front element
        if (minEle != i) {
            int temp = inArr[i];
            inArr[i] = inArr[minEle];
            inArr[minEle] = temp;
        }
    }
}

Test:

public static void main(String[] args) {
    int[] arr = {29, 24, 20, 37, 14};
    selectionSort(arr);
    for (int i = 0; i < arr.length; i++) {
        System.out.print(arr[i] + " ");
    }
}

14 20 24 29 37 

Average time complexity: $O(n^2)$
Worst time complexity: $O(n^2)$

---

4 Insertion Sort

插入排序

Algorithm:

1. Assume the first element is already sorted, start from the second element;
2. Scan the sorted elements($S$) before the current element($C$) (left in illustration) from the end to the beginning;
3. If the element $C$ is smaller than the element $S$, move the scanner to next position;
4. Repeat step 3 until the element $C$ is larger than or equal to the element $S$, then insert the element $C$ into the position.
5. Repeat step 2-4 until all elements are sorted.

Illustration:

Source: VisuAlgo

Java implementation:

public static void insertionSort(int[] inArr) {
    int n = inArr.length;
    for (int i = 1; i < n; i++) {
        int key = inArr[i]; // The element to be inserted (C)
        int j = i - 1; // The element to be compared in the sorted part (S)
        // Find the position to insert the element (C)
        while (j >= 0 && inArr[j] > key) {
            inArr[j + 1] = inArr[j];
            j--;
        }
        inArr[j + 1] = key; // Insert the element (C)
    }
}

Test:

public static void main(String[] args) {
    int[] arr = {29, 24, 20, 37, 14};
    insertionSort(arr);
    for (int i = 0; i < arr.length; i++) {
        System.out.print(arr[i] + " ");
    }
}

14 20 24 29 37 

Average time complexity: $O(n^2)$
Worst time complexity: $O(n^2)$

---

5 Merge Sort

并归排序

Algorithm:
A classic application of Divide and Conquer(分治法) algorithm.

1. Divide the array into two halves;
2. Recursively sort the two halves;
3. Merge the two sorted halves into one sorted array.

Illustration: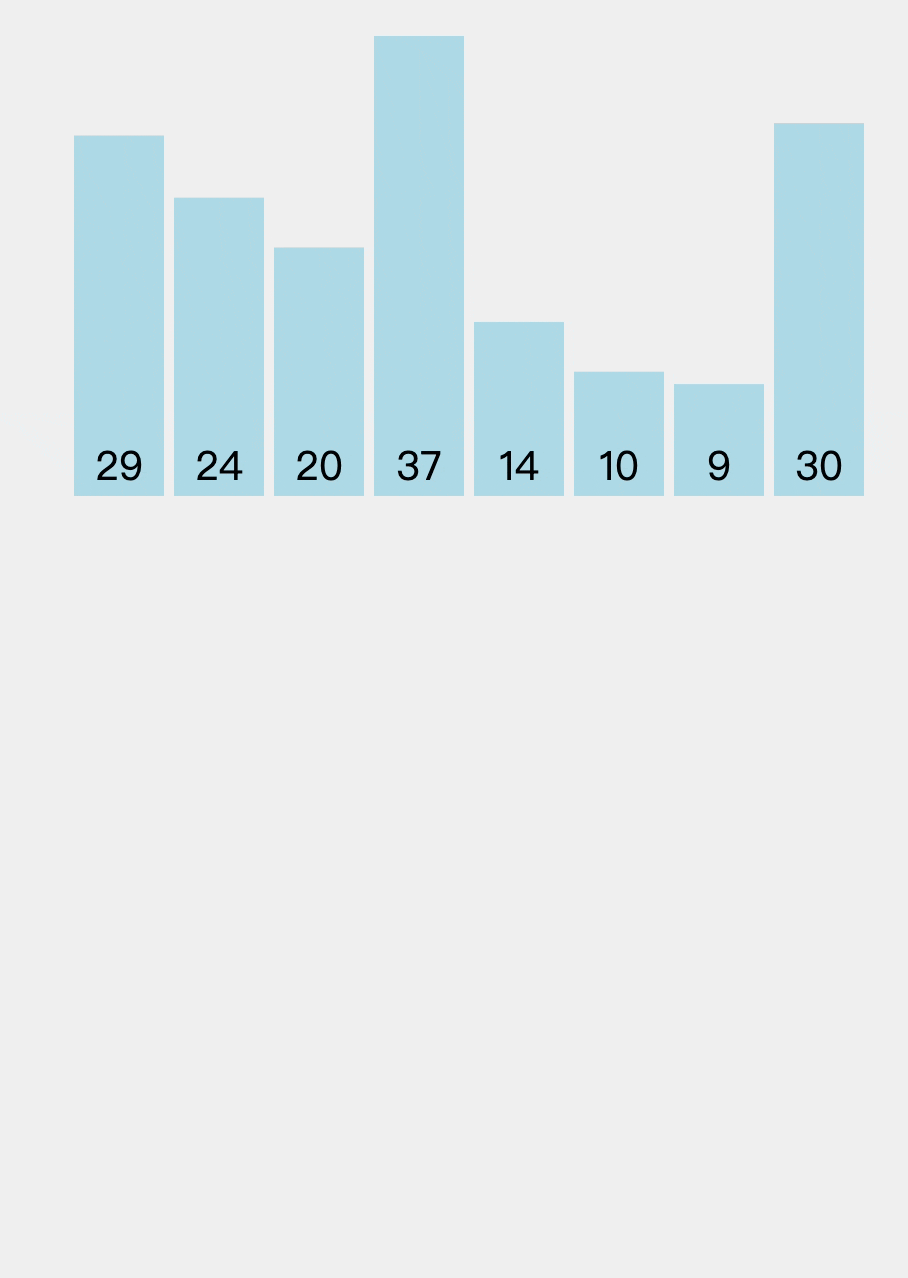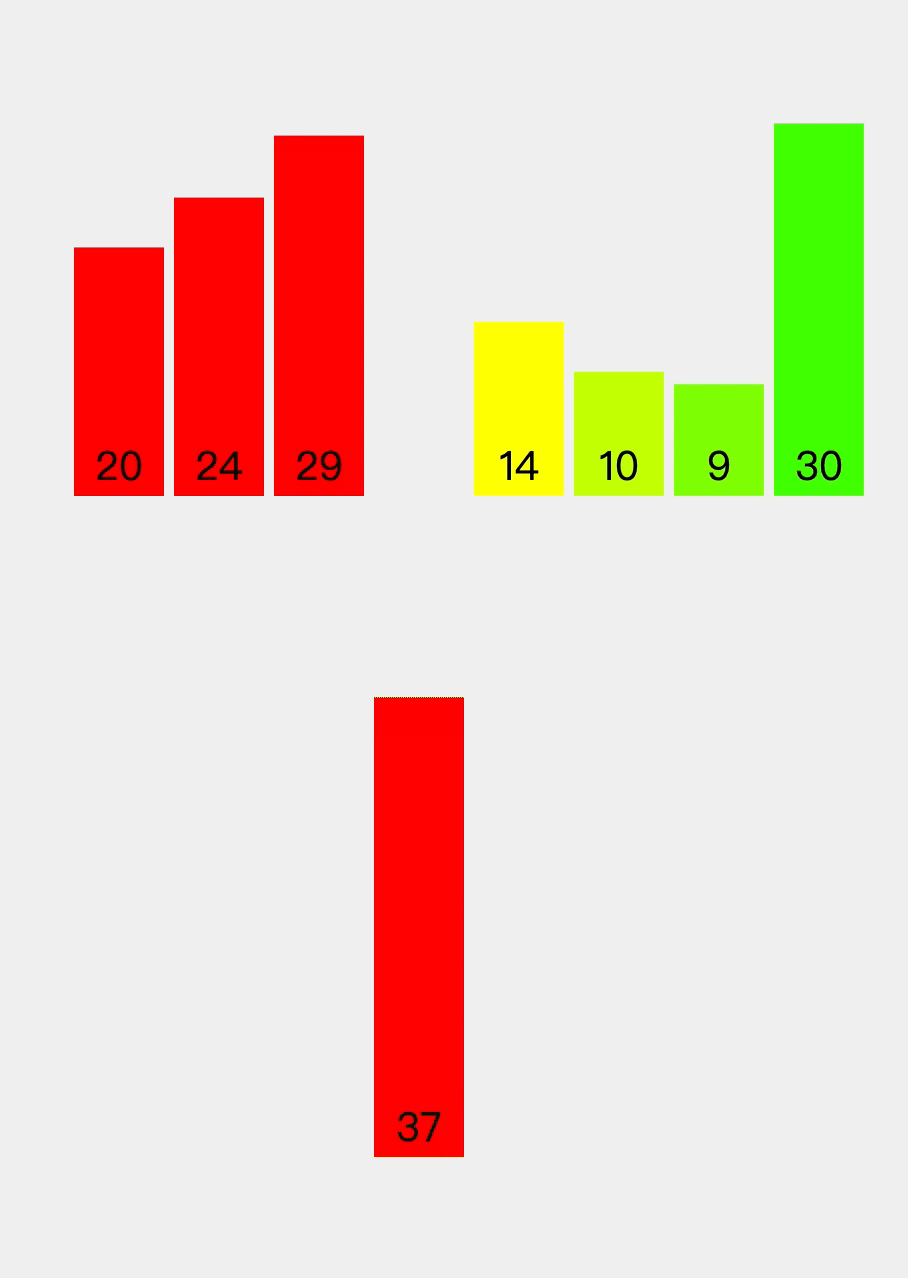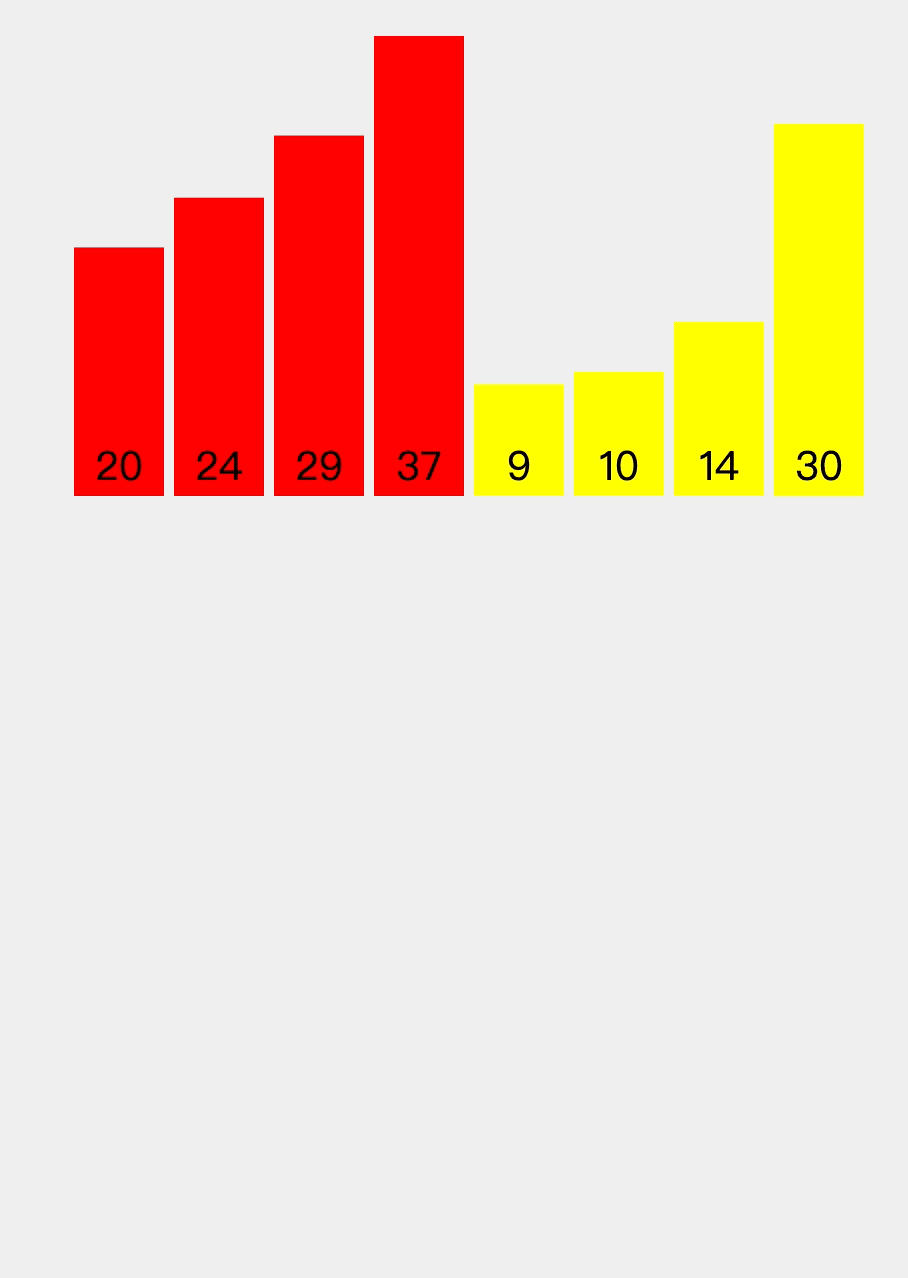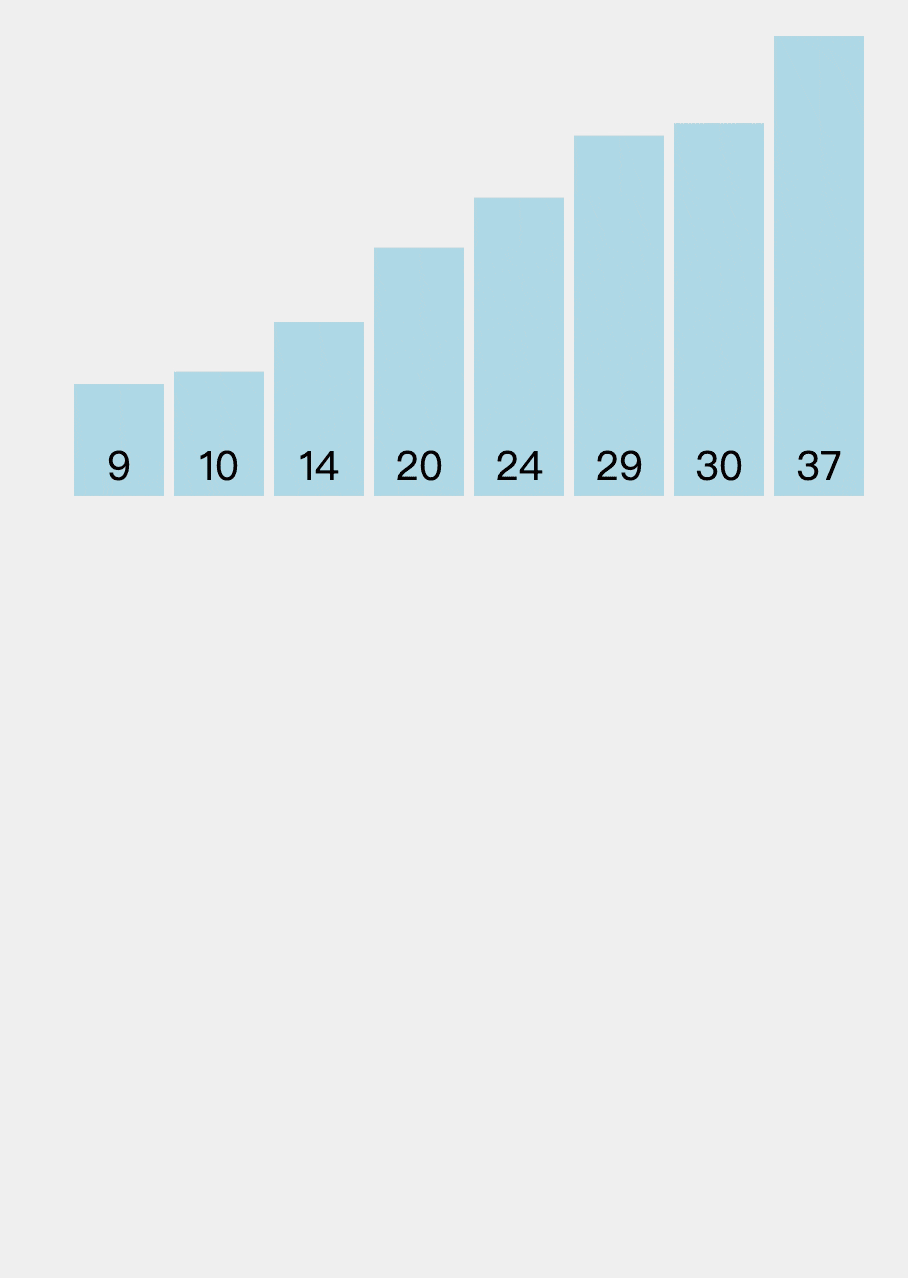

Source: VisuAlgo

Java implementation:

public static int[] mergeSort(int[] inArr) {
    int n = inArr.length;
    if (n <= 1) {
        return inArr;
    }
    // Step 1: Divide the array into two halves
    int mid = n / 2;
    int[] left = new int[mid];
    int[] right = new int[n - mid];
    for (int i = 0; i < mid; i++) {
        left[i] = inArr[i];
    }
    for (int i = mid; i < n; i++) {
        right[i - mid] = inArr[i];
    }
    // Step 2: Recursively sort the two halves
    int[] sortedLeft = mergeSort(left);
    int[] sortedRight = mergeSort(right);
    return merge(sortedLeft, sortedRight);
}

// Step 3: Merge two sorted arrays into one sorted array
public static int[] merge(int[] left, int[] right) {
    int i = 0, j = 0, k = 0;
    int[] arr = new int[left.length + right.length];
    while (i < left.length && j < right.length) {
        if (left[i] < right[j]) {
            arr[k++] = left[i++];
        } else {
            arr[k++] = right[j++];
        }
    }
    while (i < left.length) {
        arr[k++] = left[i++];
    }
    while (j < right.length) {
        arr[k++] = right[j++];
    }
    return arr;
}

Test:

public static void main(String[] args) {
    int[] arr = {29, 24, 20, 37, 14, 10, 9, 30};
    int[] sortedArr = mergeSort(arr);
    for (int i = 0; i < sortedArr.length; i++) {
        System.out.print(sortedArr[i] + " ");
    }
}

14 20 24 29 37 

Average time complexity: $O(n log(n))$
Worst time complexity: $O(n log(n))$

---

6 Quick Sort

快速排序

Algorithm:
A classic application of Divide and Conquer(分治法) algorithm.

1. Choose a pivot element (start from the first element);
2. Compare the pivot element with the rest of the elements;
3. Find all elements that are smaller than the pivot element, rearrange them in the left part of the array;
4. Find all elements that are larger than the pivot element, rearrange them in the right part of the array;
5. Now, the pivot element is in the correct position;
6. Repeat step 2-5 for the left and right parts of the array recursively.

Illustration: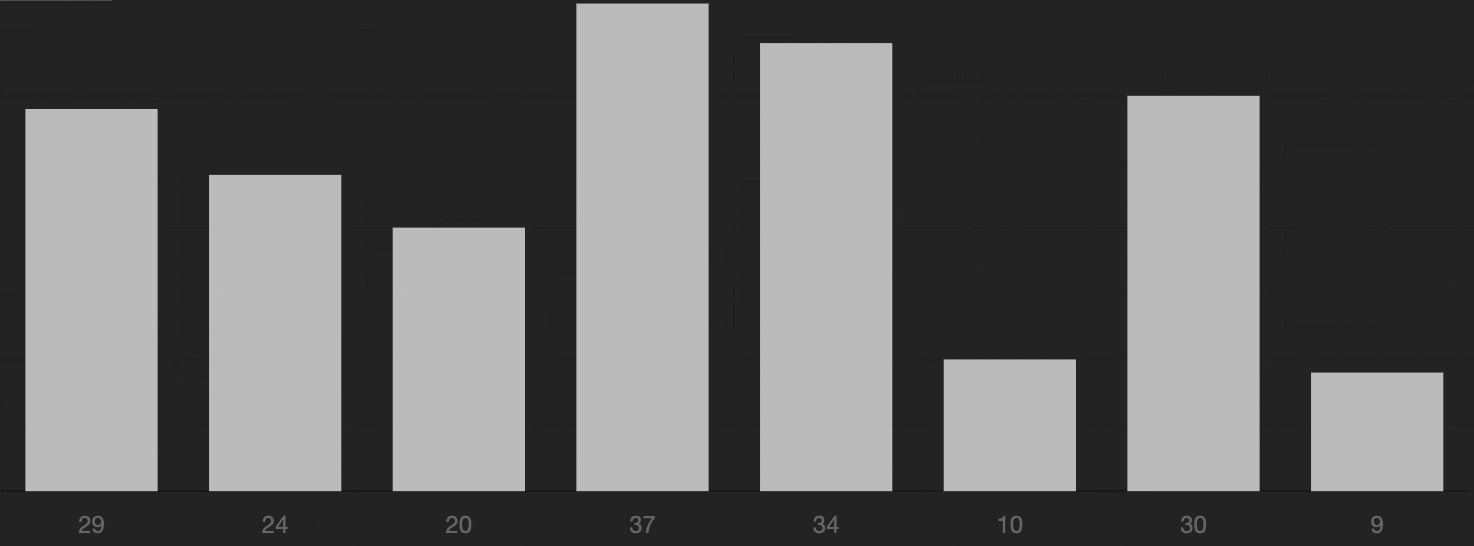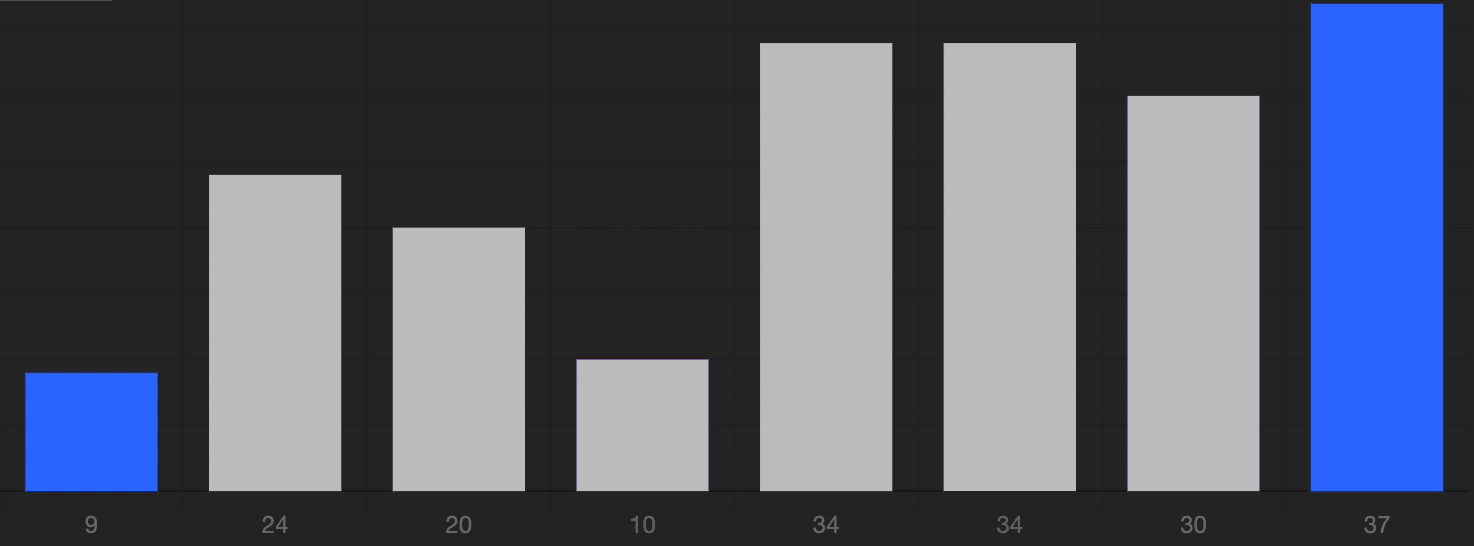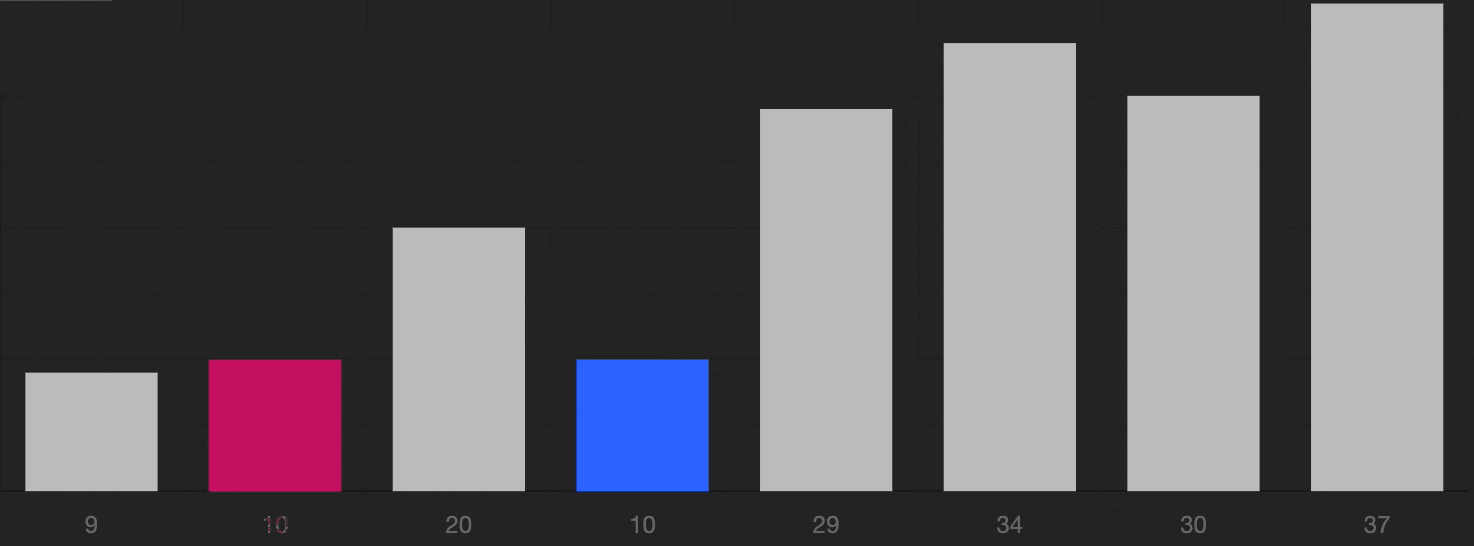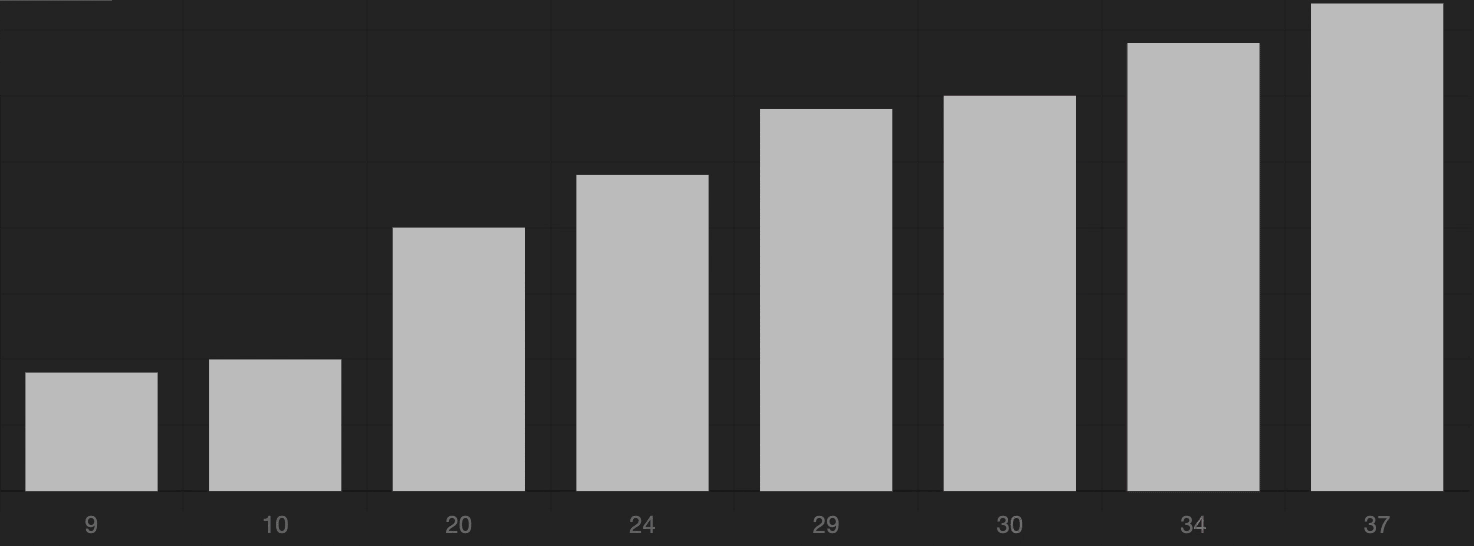

Source: Quicksort - Algorithm Visualizer

Java implementation:

public static void quickSort(int[] inArr) {
    quickSort(inArr, 0, inArr.length - 1);
}

private static void quickSort(int[] inArr, int low, int high) {
    if (low < high) {
        int pivot = partition(inArr, low, high);
        quickSort(inArr, low, pivot - 1);
        quickSort(inArr, pivot + 1, high);
    }
}

private static int partition(int[] inArr, int low, int high) {
    int pivot = inArr[low];
    while (low < high) {
        while (low < high && inArr[high] >= pivot) {
            high--;
        }
        inArr[low] = inArr[high];
        while (low < high && inArr[low] <= pivot) {
            low++;
        }
        inArr[high] = inArr[low];
    }
    inArr[low] = pivot;
    return low;
}

Test:

public static void main(String[] args) {
    int[] arr = {29, 24, 20, 37, 34, 10, 30, 9};
    quickSort(arr);
    for (int i = 0; i < arr.length; i++) {
        System.out.print(arr[i] + " ");
    }
}

9 10 20 24 29 30 34 37 

Average time complexity: $O(n log(n))$
Worst time complexity: $O(n^2)$

---

7 Counting Sort

计数排序

Very interesting sorting algorithm. More details will be discussed in later articles.

Algorithm:

1. Find the maximum element in the array (as value $M$);
2. Build a count array with size $M + 1$ (as array $C$);
3. Count the number of each element in unsorted array (as element $i$ appears $n$ times), store C[i] = n;
4. Accumulate each element in count array with the previous one (as element $i$ should appears in position of $(C[i - 1] + C[i])$) to get the final position of each element;
5. Put all elements back to the array in the correct position (the position of element $i$ is $(C[i - 1] + C[i])$);

Illustration:

Source: VisuAlgo

Java implementation:

public static void countingSort(int[] inArr) {
    int n = inArr.length;
    int max = inArr[0];
    for (int i = 1; i < n; i++) {
        if (inArr[i] > max) {
            max = inArr[i];
        }
    }
    int[] countArr = new int[max + 1];
    for (int i = 0; i < n; i++) {
        countArr[inArr[i]]++;
    }
    for (int i = 1; i < countArr.length; i++) {
        countArr[i] += countArr[i - 1];
    }
    int[] sortedArr = new int[n];
    for (int i = n - 1; i >= 0; i--) {
        sortedArr[countArr[inArr[i]] - 1] = inArr[i];
        countArr[inArr[i]]--;
    }
    for (int i = 0; i < n; i++) {
        inArr[i] = sortedArr[i];
    }
}

Test:

public static void main(String[] args) {
    int[] arr = {2,3,8,7,1,2,7,3,9,8,2,1,4};
    countingSort(arr);
    for (int i = 0; i < arr.length; i++) {
        System.out.print(arr[i] + " ");
    }
}

1 1 2 2 2 3 3 4 7 7 8 8 9 

Average time complexity: $O(n+k)$
Worst time complexity: $O(n+k)$

---

8 Heap Sort

堆排序

Algorithm:
Very similar to selection sort, but instead of using linear scan to find the maximum element, we use heap data structure to find the maximum element.

Heap:
A binary tree whose root is the largest element in the tree, and the value of each vertex (except the root) is greater than the value of its child vertices.

Illustration:

Heap Sort - Algorithm Visualizations

Java implementation:

public static void heapSort(int[] inArr) {
    int n = inArr.length;
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(inArr, n, i);
    }
    for (int i = n - 1; i >= 0; i--) {
        int temp = inArr[0];
        inArr[0] = inArr[i];
        inArr[i] = temp;
        heapify(inArr, i, 0);
    }
}

private static void heapify(int[] inArr, int n, int i) {
    int largest = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    if (l < n && inArr[l] > inArr[largest]) {
        largest = l;
    }
    if (r < n && inArr[r] > inArr[largest]) {
        largest = r;
    }
    if (largest != i) {
        int temp = inArr[i];
        inArr[i] = inArr[largest];
        inArr[largest] = temp;
        heapify(inArr, n, largest);
    }
}

Test:

public static void main(String[] args) {
    int[] a = {29, 24, 20, 37, 14};
    heapSort(a);
    for (int i = 0; i < a.length; i++) {
        System.out.print(a[i] + " ");
    }
}

14 20 24 29 37 

Average time complexity: $O(n log(n))$
Worst time complexity: $O(n log(n))$

---

9 Summary

Sort Algorithm	Average Time Complexity	Worst Time Complexity
Bubble Sort	$O(n^2)$	$O(n^2)$
Selection Sort	$O(n^2)$	$O(n^2)$
Insertion Sort	$O(n^2)$	$O(n^2)$
Merge Sort	$O(n log(n))$	$O(n log(n))$
Quick Sort	$O(n log(n))$	$O(n^2)$
Counting Sort	$O(n+k)$	$O(n+k)$
Heap Sort	$O(n log(n))$	$O(n log(n))$

Source: Big-O Cheat Sheet

---

References

Algorithm Visualizer
Big-O Cheat Sheet
M. Goodrich, R. Tamassia, and A. O’reilly, Data Structures and Algorithms in Java, 6th Edition. John Wiley & Sons, 2014.
R. Sedgewick and K. Wayne, Algorithms. Upper Saddle River, Nj: Addison-Wesley, 2011.
十大经典排序算法大梳理 (动图+代码)
visualising data structures and algorithms through animation - VisuAlgo

---

写在最后

还有很多有趣的排序算法，如Bucket Sort, Radix Sort, Shell Sort，会继续学习，继续更新。
最后，希望大家一起交流，分享，指出问题，谢谢！

---

原创文章，转载请标明出处
Made by Mike_Zhang

感谢你的支持