Limits and Continuity Note

Made by Mike_Zhang

---

所有文章:
Introductory Probability Course Note
Python Basic Note
Limits and Continuity Note
Calculus for Engineers Course Note
Introduction to Data Analytics Course Note
Introduction to Computer Systems Course Note

---

个人笔记，仅供参考
FOR REFERENCE ONLY

---

1. Limits

1.1 Definition of Limits

Limit of $f(x)$ as x approaches $c$ is the number $L$:

$$\lim_{x\to c}f(x)=L$$

$f(x)$ is defined on open interval about $c$ (exclusive)
$\forall \epsilon \gt 0, \;\exists \delta > 0$ such that $\forall x$,

$$0\lt |x-c| \lt \delta \implies |f(x)-L| \lt \epsilon$$

To find a $\delta$ for a Given $f,L,c$ and $\epsilon \gt 0$:

1. solve $|f(x)-L| \lt \epsilon$ to get a open interval $(a,b)$ containing $c$;
2. Find a $\delta \gt 0$ placing the interval $(c-\delta, c+\delta)$ centered at $c$ inside the interval $(a,b)$.

1.2 Theorems of Limits

if $f(x) = x$ (identity function),

$$\lim_{x\to c}f(x)=\lim_{x\to c}x = c$$

if $f(x) = k$ (constant function),

$$\lim_{x\to c}f(x)=\lim_{x\to c}k = k$$

---

1.2.1 Limits Laws

Set

$$\lim_{x\to c}f(x)=L\;and\;\lim_{x\to c}g(x)=M$$

1. Sum Rule: $\lim_{x\to c}(f(x)+g(x))=L+M$
2. Difference Rule: $\lim_{x\to c}(f(x)-g(x))=L-M$
3. Constant Multiple Rule: $\lim_{x\to c}(k\cdot f(x))=k\cdot L$
4. Product Rule: $\lim_{x\to c}(f(x)\cdot g(x))=L\cdot M$
5. Quotient Rule: $\lim_{x\to c}\frac{f(x)}{g(x)}=\frac{L}{M}\;(M\ne0)$
6. Power Rule: $\lim_{x\to c}[f(x)]^n=L^n\; (n \in Z^+)$
7. Root Rule: $\lim_{x\to c}\sqrt[n]{f(x)}=\sqrt[n]L\; (n \in Z^+)$

---

1.2.2 Limits of Polynomials

$$P(x) = a_nx^n + a_{n-1}x^{n-1}+ ... + a_0$$

then,

$$\lim_{x\to c}P(x)=P(c) = a_nc^n + a_{n-1}c^{n-1}+ ... + a_0$$

---

1.2.3 Limits of Rational Functions

Polynomials $P(x)$, $Q(x)$ and $Q(x) \ne 0$:

$$\lim_{x\to c}\frac{P(x)}{Q(x)}=\frac{P(c)}{Q(c)}$$

If the denominator is 0, cancel the common factors in the numerator and denominator, then use that theorem.
To find the common factor:
If Polynomials $Q(x)$ and $Q(c) = 0$, if $P(c) = 0$ too, then the common factor is $(x-c)$

---

1.2.4 Sandwich Theorem

$\forall x,\;g(x)\le f(x)\lt h(x)$ in some open interval containing $c$, except at $x=c$,

$$\lim_{x\to c}g(x)=\lim_{x\to c}h(x)=L$$

Then,

$$\lim_{x\to c}f(x)=L$$

---

1.2.5

$\forall x,\;f(x)\le g(x)$ in some open interval containing $c$, except at $x=c$ and both limits exist,

$$\lim_{x\to c}f(x)\le \lim_{x\to c}g(x)$$

---

2. One-Sided Limits

2.1 Definition of One-Sided Limits

1. Right-hand limits
   $f(x)$ defined on $(c,b)$, where $c\lt b$, $f(x)$ has right-hand limits $L$ at $c$: $\lim_{x\to c^+}f(x)=L$
   if, $\forall \epsilon \gt 0$, $\exists \delta \gt 0$ such that $\forall x$: $c\lt x \lt c+\delta \implies |f(x)-L|\lt \epsilon$
2. Left-hand limits
   $f(x)$ defined on $(a,c)$, where $a\lt c$, $f(x)$ has left-hand limits $M$ at $c$: $\lim_{x\to c^-}f(x)=M$
   if, $\forall \epsilon \gt 0$, $\exists \delta \gt 0$ such that $\forall x$: $c-\delta\lt x \lt c \implies |f(x)-M|\lt \epsilon$

2.2 Theorem of One-Sided Limits

2.2.1

$$\lim_{x\to c}f(x)=L \iff \lim_{x\to c^+}f(x)=L \;\;\;and\;\;\; \lim_{x\to c^-}f(x)=L$$

---

2.2.2 Limits of the Ratio $sin \theta/\theta$ as $\theta \rightarrow 0$

$$\lim_{\theta \to 0} \frac{\sin{\theta}}{\theta}=1$$

($\theta$ in radians)

---

3. Continuity

3.1 Definition of Continuity of f(x)

1. $f$ is continuous at $c$ if: $$\lim_{x\to c}f(x)=f(c)$$
2. $f$ is right-continuous at $c$ if: $$\lim_{x\to c^+}f(x)=f(c)$$
3. $f$ is left-continuous at $c$ if: $$\lim_{x\to c^-}f(x)=f(c)$$

---

3.2 Continuity Test

$f$ is continuous at $c$ $\iff$

1. $f(c)$ exits ($c$ in the domain) and,
2. $\lim_{x\to c}f(x)$ exits and,
3. $\lim_{x\to c}f(x)=f(c)$

---

3.3 Theorem of Continuity

3.3.1 Properties of Continuous Functions

If $f$ and $g$ are continuous at $x=c$, then the combination using 1.2.1 Limits Laws are continuous at $x=c$.

---

3.3.2 Polynomials Continuity

Polynomials

$$P(x) = a_nx^n + a_{n-1}x^{n-1}+ ... + a_0$$

is continuous, for $\lim_{x\to c}P(x)=P(c)$.

---

3.3.3 Rational Functions Continuity

Rational Functions
Polynomials $P(x)$, $Q(x)$ and $Q(x) \ne 0$:

$$\lim_{x\to c}\frac{P(x)}{Q(x)}=\frac{P(c)}{Q(c)}$$

is continuous.

---

3.3.4 Inverse Function Continuity

The inverse function of any function continuous on an interval is continuous over its domain.

---

3.3.5 Composite of Continuous Functions

$f$ is continuous at $c$ and $g$ is continuous at $f(c)\implies$ the composite $g\circ f$ is continuous at $c$.

---

3.3.6 Limits of Continuous Functions

$g$ is continuous at $b$ and $\lim_{x\to c}f(x)=b$,

$$\lim_{x\to c}g(f(x))=g(b)=g(\lim_{x\to c}f(x))$$

---

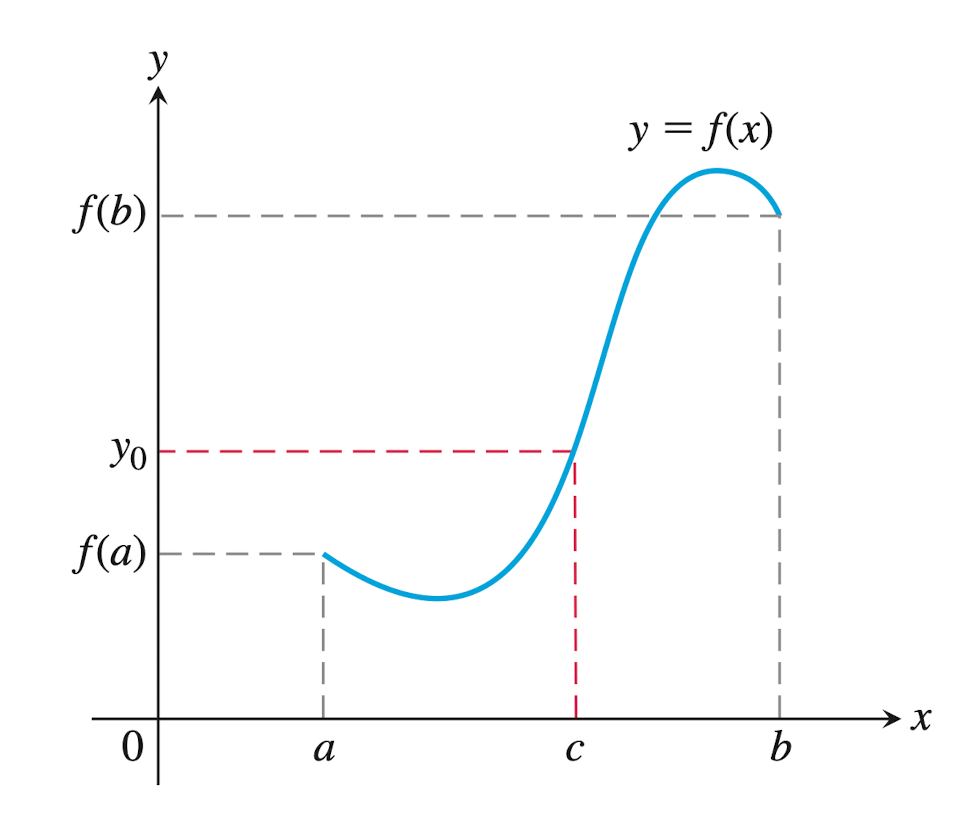
3.3.7 The Intermediate Value Theorem for Continuous Functions

If $f$ is continuous on interval $[a,b]$, and if $y_0$ is any value between $f(a)$ and $f(b)$, then $y_0=f(c)$ for some $c$ in $[a,b]$.

Intermediate Value Theorem - Thomas' calculus: early transcendentals (Thirteenth edition)

---

4. Infinity Limits & Asymptotes

4.1 Definition of Infinity Limits

1. $f(x)$ has limit $L$ as x approaches infinity: $\lim_{x\to \infty}f(x)=L$
   if, $\forall \epsilon \gt 0$, $\exists M $ such that $\forall x$: $x \gt M \implies |f(x)-L|\lt \epsilon$
2. $f(x)$ has limit $L$ as x approaches minus infinity: $\lim_{x\to -\infty}f(x)=L$
   if, $\forall \epsilon \gt 0$, $\exists N $ such that $\forall x$: $x \lt N \implies |f(x)-L|\lt \epsilon$

$$\lim_{x\to \pm \infty}k=k \;\; and \;\; \lim_{x\to \pm \infty}\frac{1}{x}=0$$

4.2 Theorems for Infinity Limits

4.2.1 Limit Laws

All Limit Laws in 1.2.1 are also applied to Infinity Limits.

---

4.2.2 limits at infinity of rational Functions

Divide the numerator and denominator by the highest power of $x$ in the denominator, then depends on the degrees of the polynomials involved.

---

4.3 Horizontal Asymptotes

A line $y = b$ is the Horizontal Asymptotes of $y=f(x)$, if

$$\lim_{x\to \infty}f(x)=b\;\;or\;\;\lim_{x\to -\infty}f(x)=b$$

---

4.4 Oblique Asymptotes

If the degree of the numerator of a rational function is 1 greater than the degree of the denominator, the graph has an oblique or slant line asymptote.

---

4.5 Vertical Asymptotes

A line $y = a$ is the Vertical Asymptotes of $y=f(x)$, if

$$\lim_{x\to a^+}f(x)=\pm \infty\;\;or\;\;\lim_{x\to a^-}f(x)=\pm \infty$$

---

4.6 Infinite Limits

4.6.1 Definitions of Infinite Limits

1. $f(x)$ approaches infinity limits as $x$ approaches $c$: $$\lim_{x\to c}f(x)=\infty=\lim_{x\to 0^+}\frac{1}{x}$$ if, $\forall B \gt 0$, $\exists \delta $ such that $\forall x$: $$0\lt |x-c|\lt \delta \implies f(x)\gt B$$
2. $f(x)$ approaches minus infinity limits as $x$ approaches $c$: $$\lim_{x\to c}f(x)=-\infty=\lim_{x\to 0^-}\frac{1}{x}$$ if, $\forall -B \lt 0$, $\exists \delta $ such that $\forall x$: $$0\lt |x-c|\lt \delta \implies f(x)\lt -B$$

---

References

Weir, Hass, Thomas, Hass, Joel, & Thomas, George B. (2014). Thomas’ calculus: early transcendentals (Thirteenth edition). Pearson.

---

个人笔记，仅供参考，转载请标明出处
FOR REFERENCE ONLY

Made by Mike_Zhang