Made by Mike_Zhang

Unfold Machine Learning Algorithm Topics | 展开机器学习算法主题 >

Intro

导言

首先思考以下情景问题：

在一个平面上，给出如下图左图的一些点，如何将这些点分成如右图的三组，也就是让每组内的点尽可能的接近，而每组之间的点尽可能的远离？

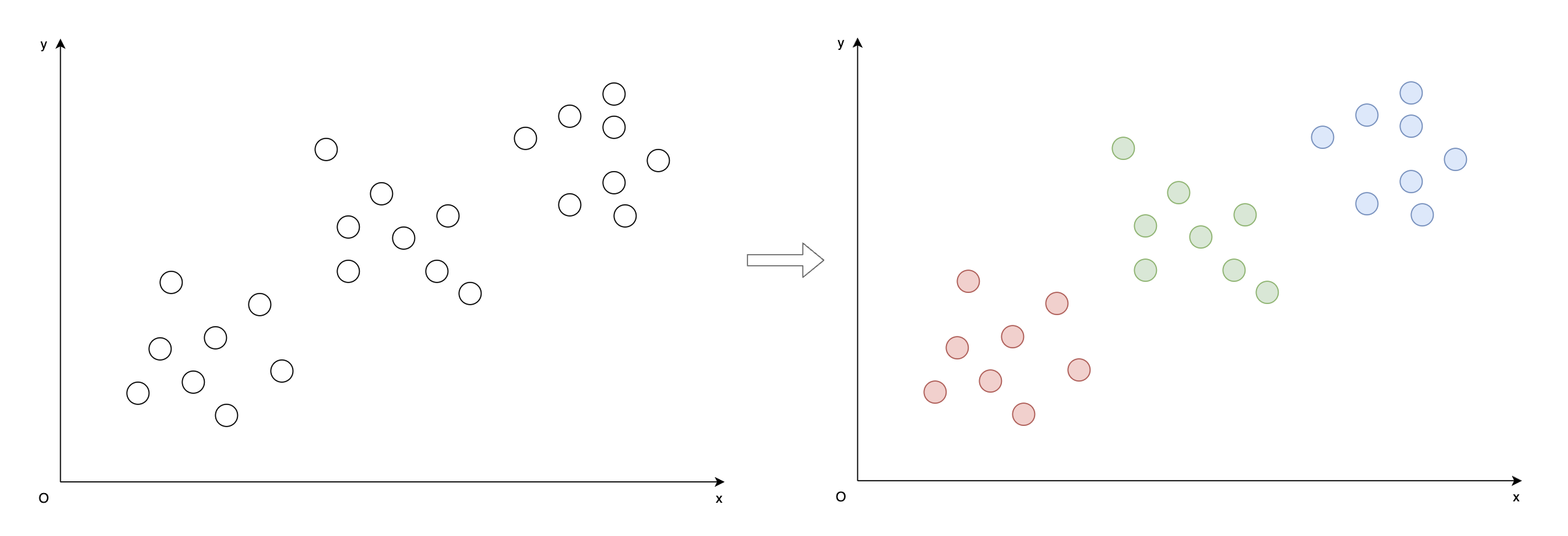
看似很容易，我们人类视觉具有接近性 (Proximity)，相近的物体会更加容易被组合在一起。

但是对于计算机来说，这些点无疑只是一堆数字，或是给定在坐标系中的坐标，那它又是如何将这些点组合的？

在计算机科学中，这类问题被称为聚类 (Clustering)，旨在把向量按照一定标准分成多个簇，同一个簇内的向量尽可能的接近。

而 k-均值算法(K-Means Clustering) 是一种经典的聚类算法。

1. K-Means Clustering Algorithm Description

1. k-均值算法描述

k-均值算法十分容易理解，其基本逻辑为：

在 选择每个簇的代表向量 与 更新每个簇的向量分配 之间进行迭代，直到所有簇收敛；
Iterating between choosing the group representatives and choosing the group assignments ¹.

具体算法如下：

给定有$N$个向量的列表，$x_1, x_2, \cdots, x_N$，以及簇的个数$k$，并随机初始化每个簇的代表向量$z_1, z_2, \cdots, z_k$。
重复：
1. 更新每个簇的分配：对于各个向量$x_i$，找到与向量 $x_i$ 最近的簇代表向量$z_j$，并把此向量$x_i$分配到$J_j$簇;
  $j= argmin_{j'}\lVert x_i-z_{j'}\rVert$
2. 更新每个簇的代表向量: 对于每个簇$J_j$，计算簇内向量的平均向量，并使其变为此簇的代表向量。
  $z_j=\frac{1}{|J_j|}\sum_{i\in J_j}x_i$

直到所有簇收敛：每个簇的代表向量不再发生变化。

1.2 Example

1.2 例子

在二维坐标系中给定以下24个向量，$N=24$，目标是将其分成三个簇，$K=3$。

Step1

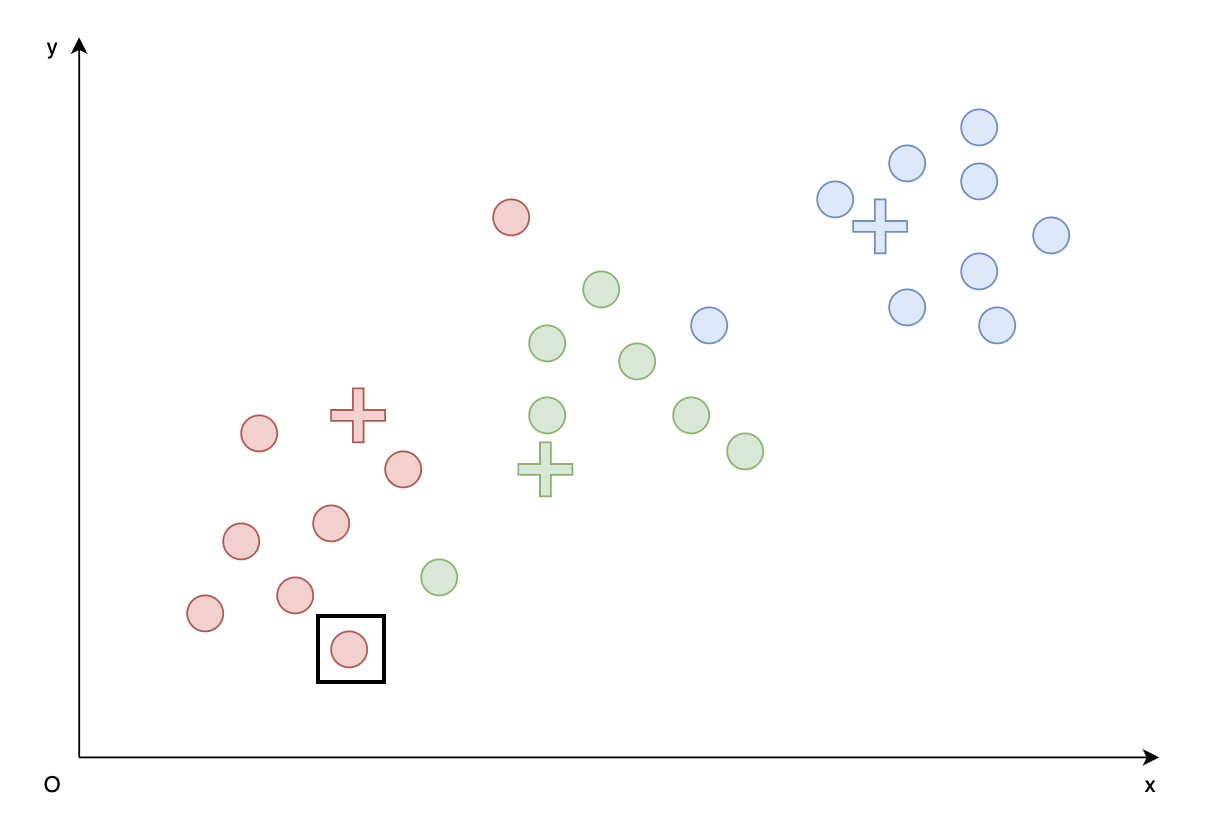
随机初始化三个簇的代表向量$z_1, z_2, z_3$，如下图三个 “$+$” 所示。

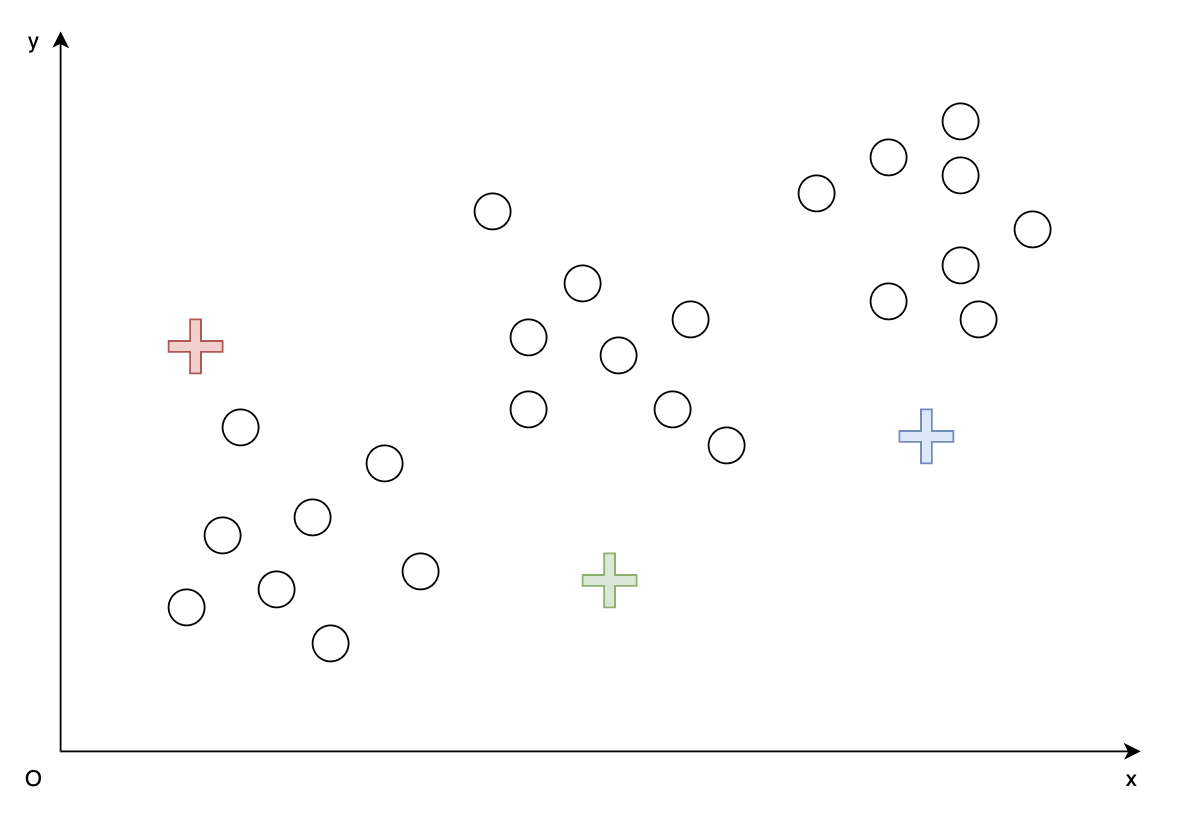
Step2

遍历所有向量，找到与向量最近的簇代表向量，并将其分配到此簇。如下图颜色分配所示。

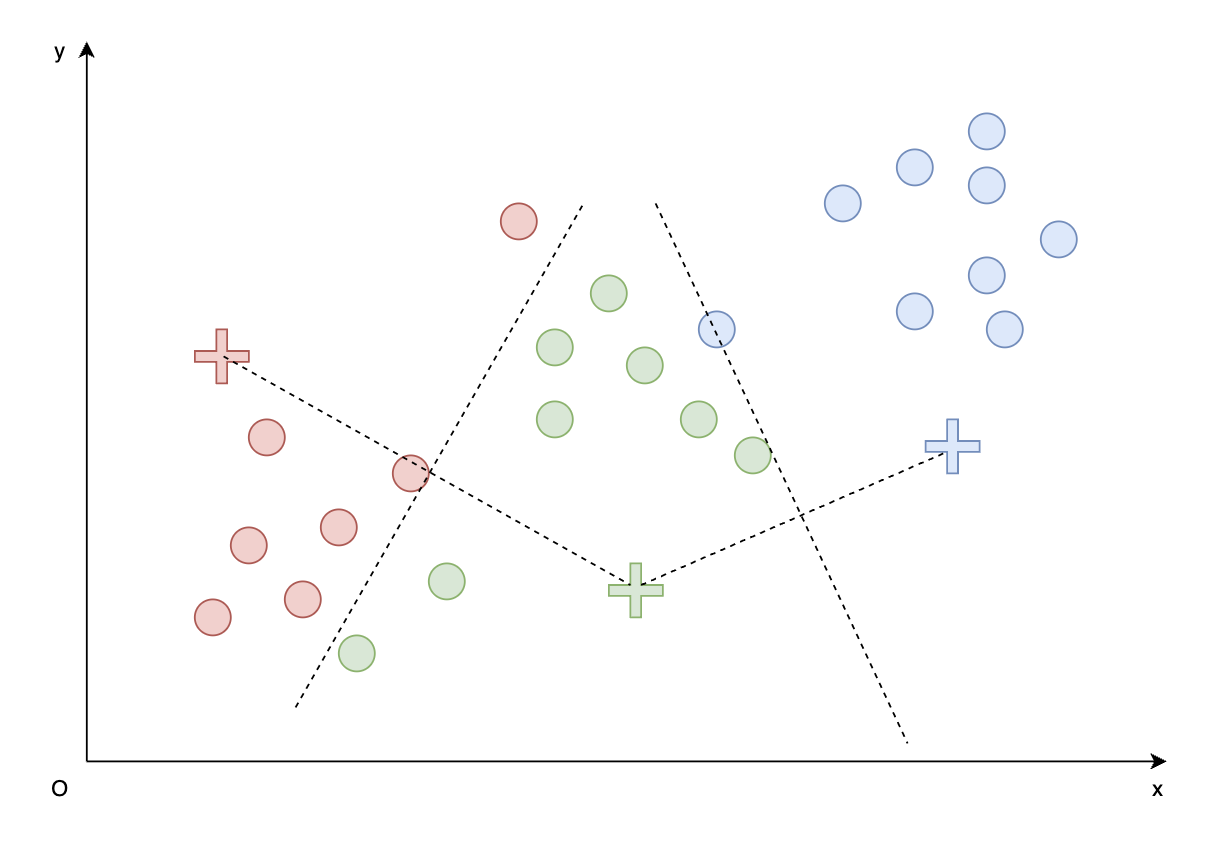
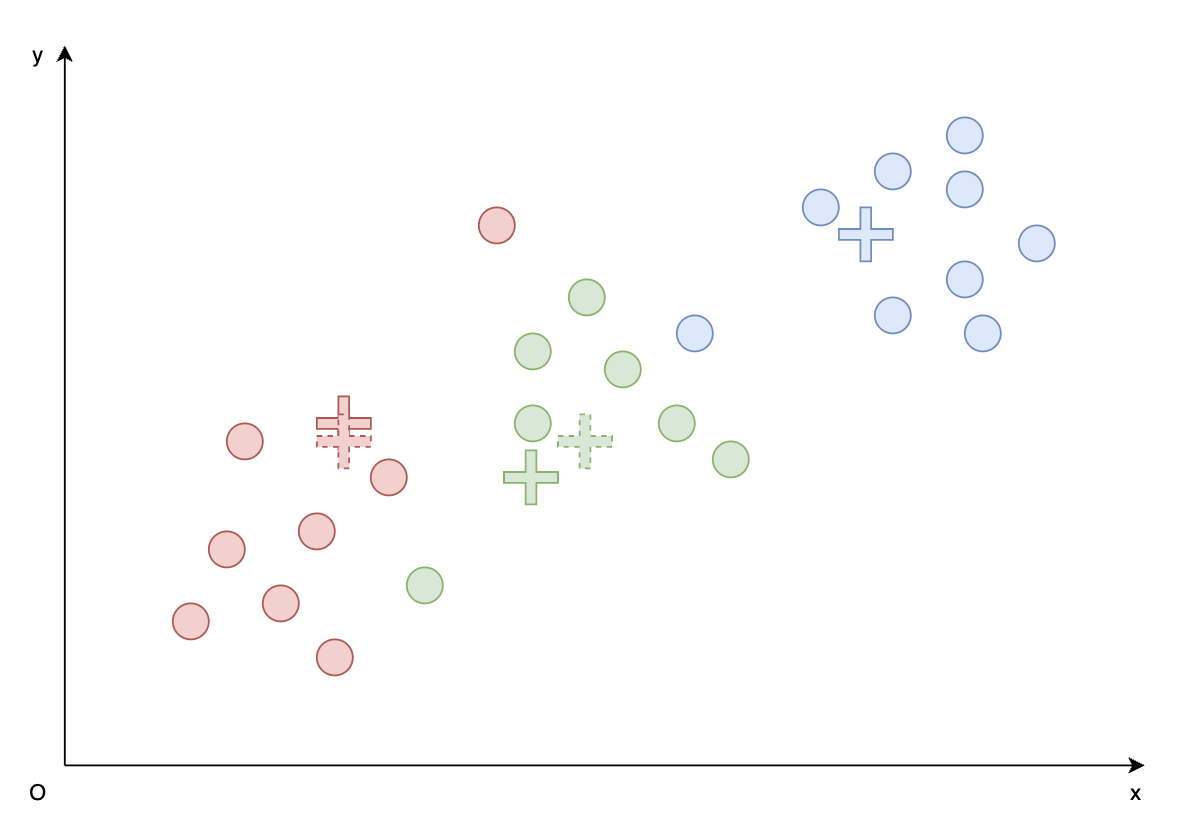
Step3

计算每个簇内向量的平均向量，下图中新代表向量以虚线 “$+$” 所示；
并使每个新代表向量成为此簇的代表向量。

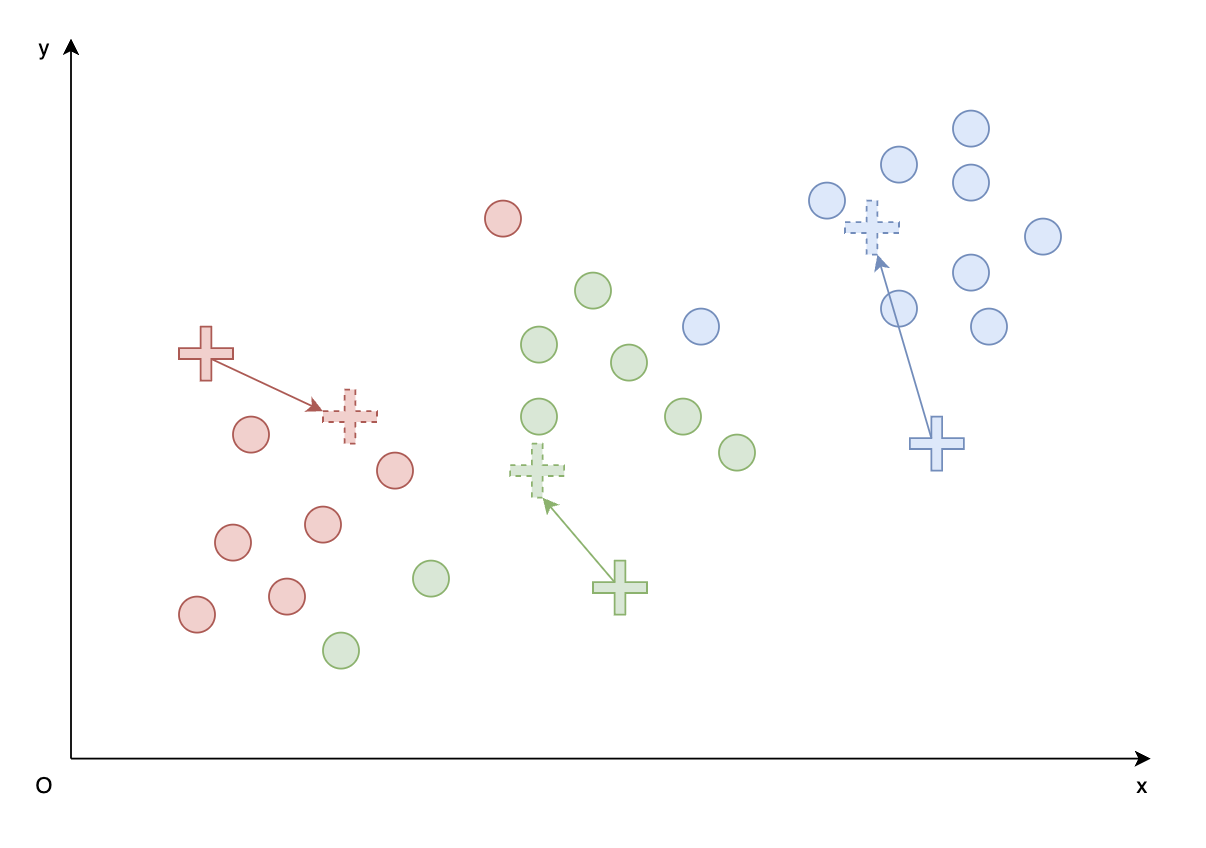
Step4

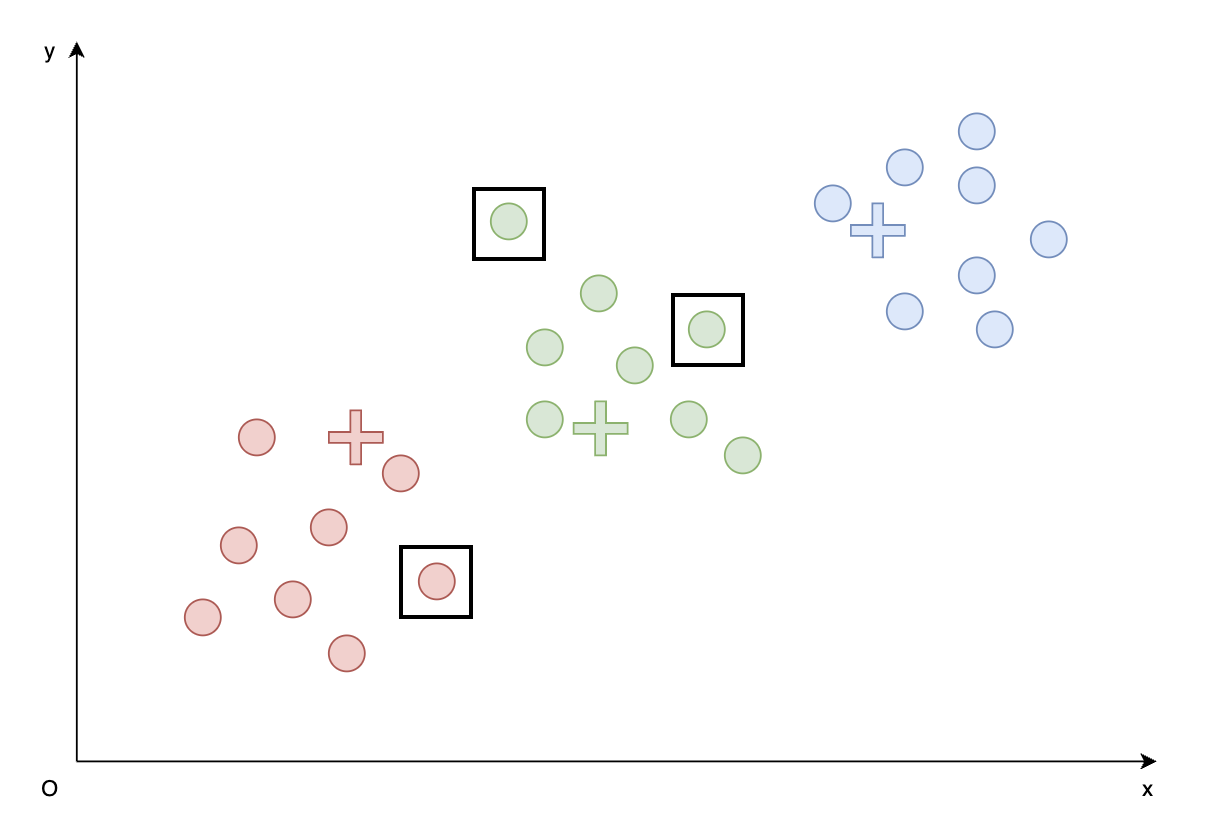
重复Step2和Step3。
- Step2. 更新每个簇的分配，黑框内的向量被重新分配：
- Step3. 计算并更新每个簇的代表向量：
- Step2. 更新每个簇的分配，黑框内的向量被重新分配：
- Step3. 计算并更新每个簇的代表向量：

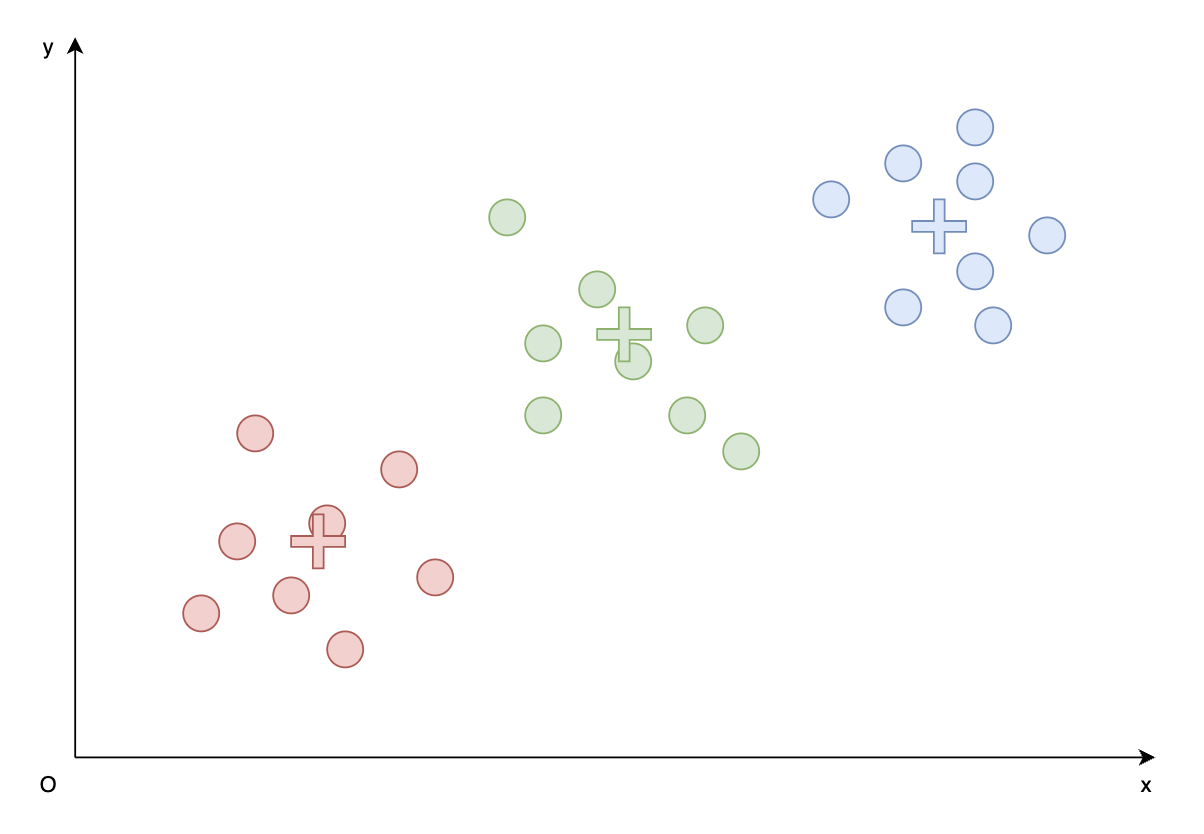
Step5

再次重复Step2和Step3，发现每个簇的代表向量不再发生变化，代表已经收敛了。
算法结束，上图就为最终的聚类结果。

2 Implementation in Python

以下是我用Python实现的k-均值算法的结果：

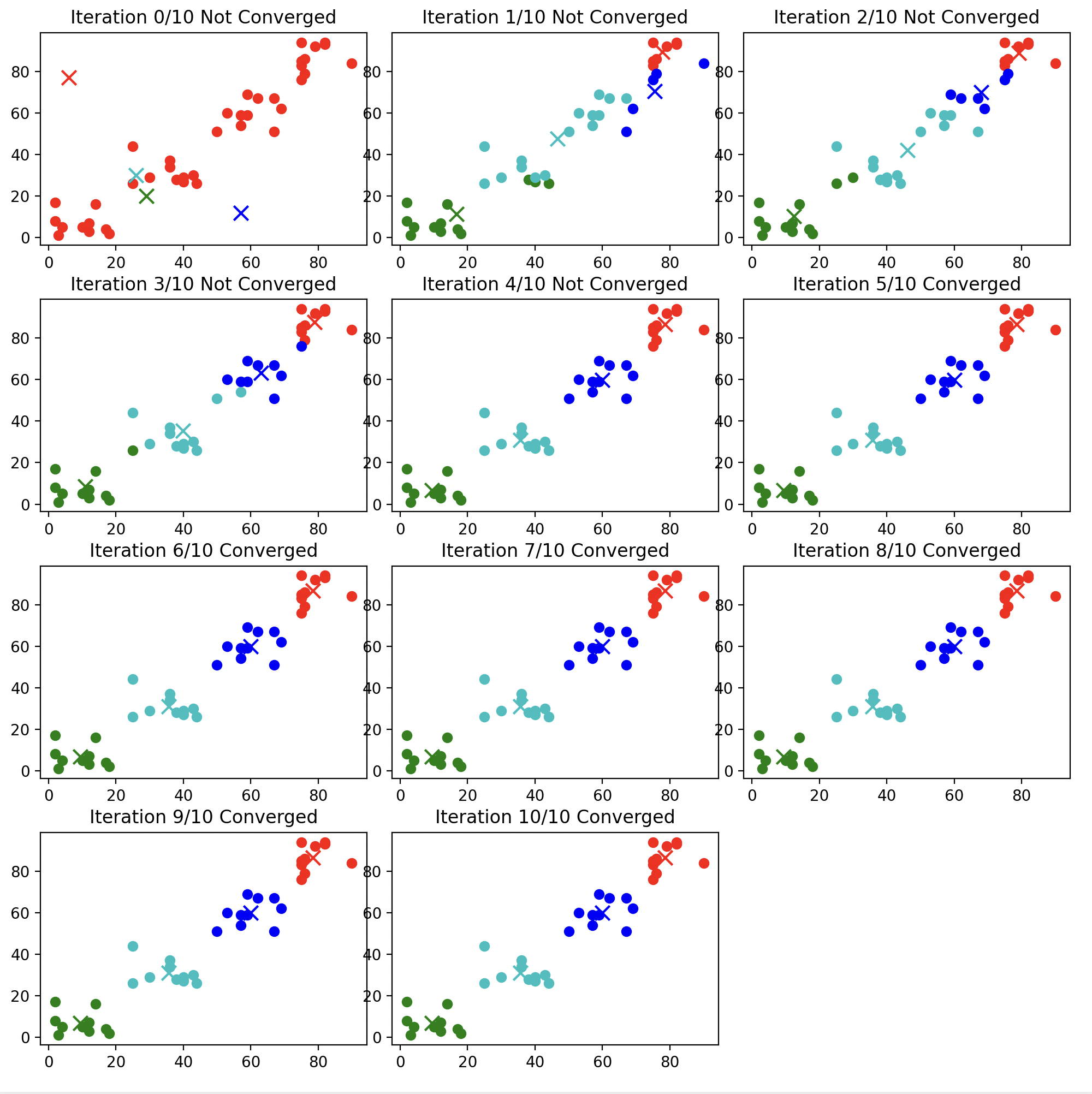
可以发现结果还是十分明显的。

代码分享在Google Colab中，点击链接可查看代码并在线运行。

3 Limitations

3. 局限性

k-均值算法是典型的一个无监督学习算法(Unsupervised Learning)，k-均值算法也有一些局限性：

1.k-均值算法必须给定簇的个数$K$，让算法随机选择$K$或者人为给定不合适的$K$，会导致算法的结果不理想。

例如，对于上面代码中的例子($K=4$)，以下为$K=3$和$K=5$时的聚类结果：

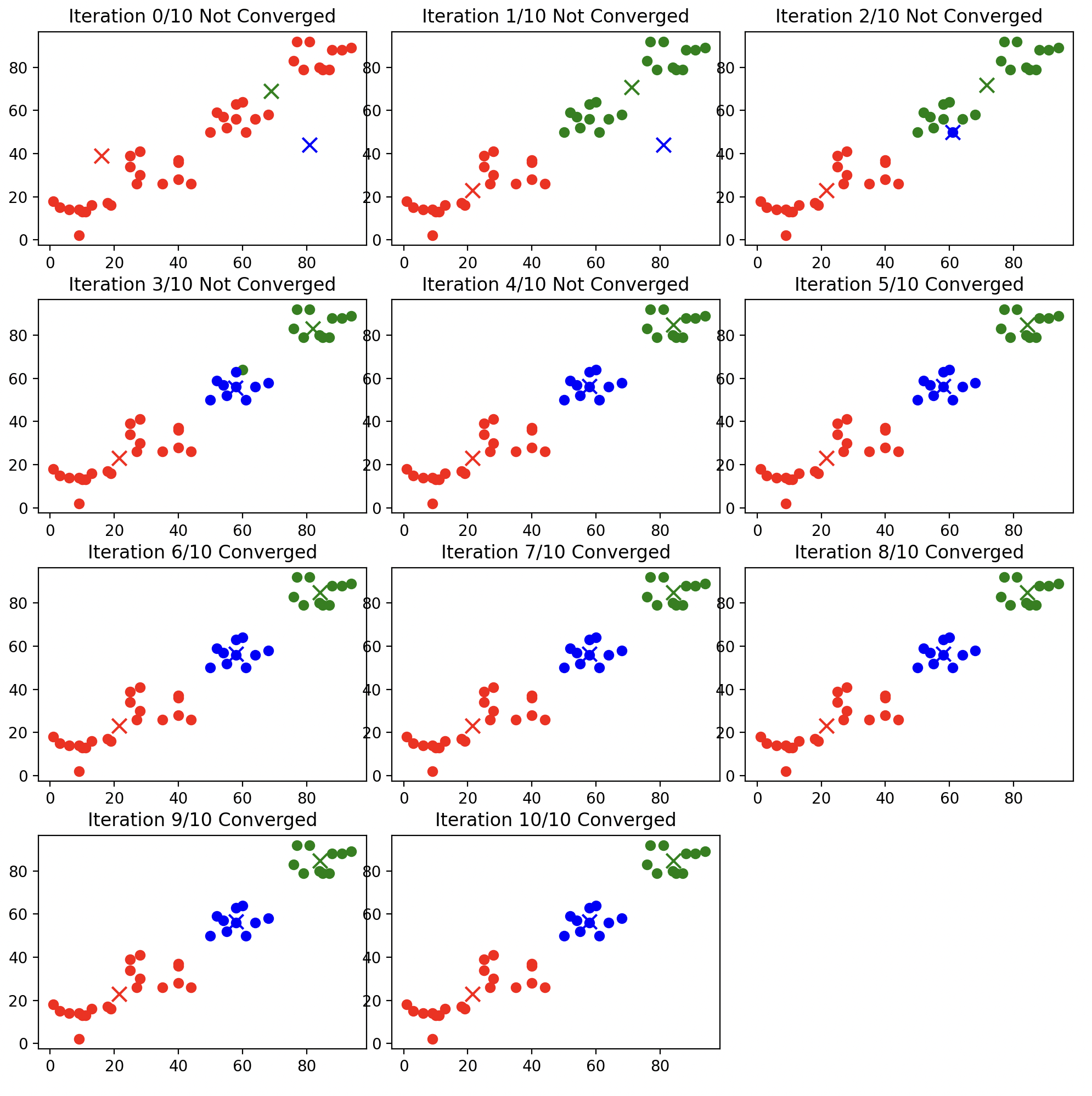
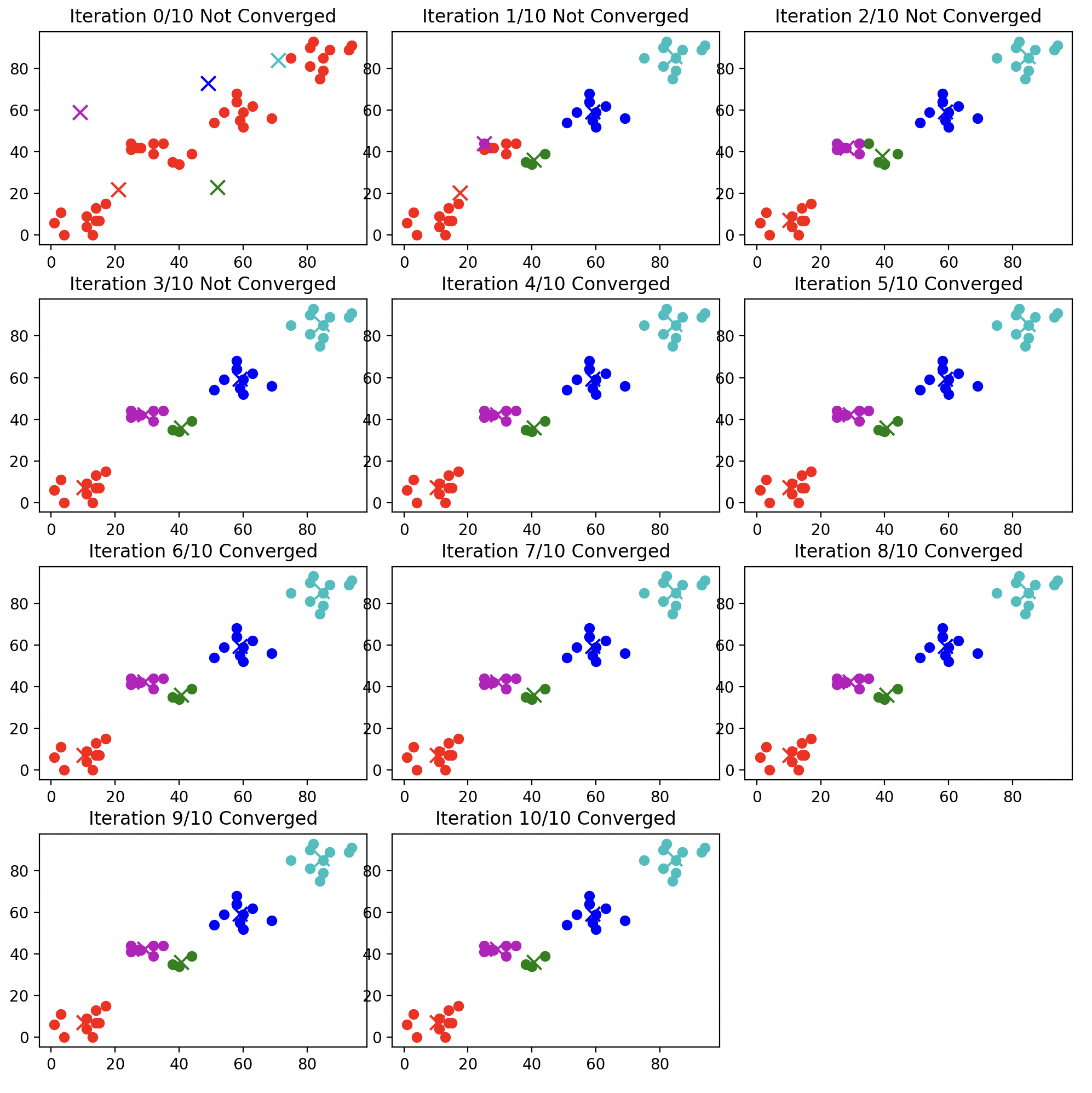
2.因为每个簇的代表向量是随机初始化的，因此每次运行k-均值算法的结果都不一样。并且初始化的代表向量的选择也会影响最终的聚类结果。

例如，对于上面的例子，在保持$K=4$，循环次数为10，有近似向量集的情况下，运行会出现以下结果：

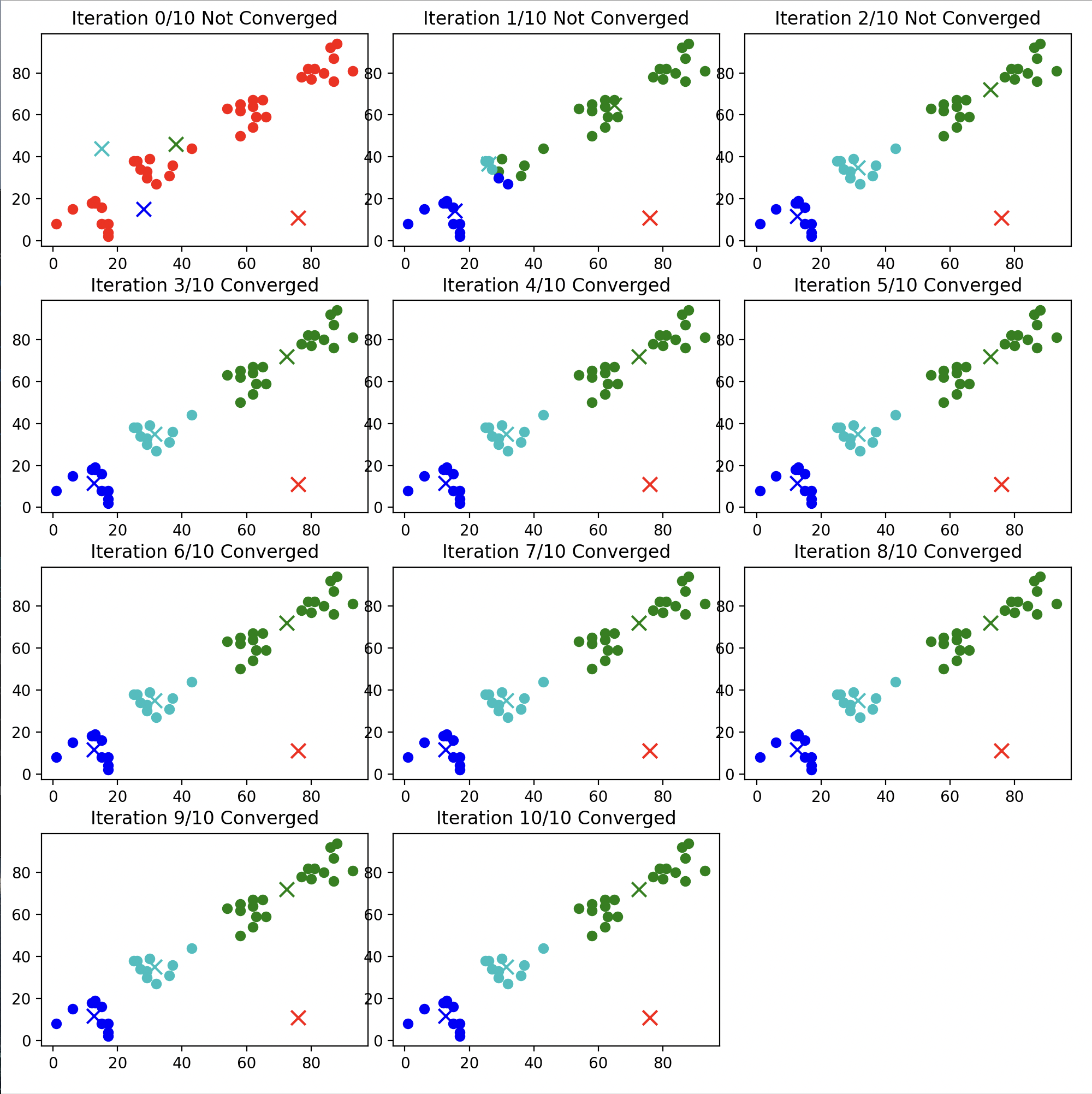
被初始化在边缘的红色代表向量，因离其他簇的向量较远，始终得不到更新。

Outro

尾巴

聚类算法，及其典型的k-均值算法有非常多的应用场景，例如，Image clustering, Document topic discover, Recommendation engine, Guessing missing entries等。
有关算法及其应用会继续学习研究，欢迎大家一起交流。

References

参考资料

¹. S. P. Boyd and Lieven Vandenberghe, Introduction to applied linear algebra : vectors, matrices, and least squares. Cambridge: Cambridge University Press, 2018. ↩

“StatQuest: K-means clustering,” www.youtube.com. https://youtu.be/4b5d3muPQmA (accessed Feb. 13, 2023).

原创文章，转载请标明出处
Made by Mike_Zhang