General Tree Introduction - 一般树简介

Made by Mike_Zhang

---

数据结构与算法主题：

---

1. Introduction

1.1 Tree Definition

Tree is one of the most important non-linear data structures. Each element in a tree sequence has a hierarchial relationship, which means that, expect the top element, each element has a parent element and zero or more children elements (each element can be “above” or “below” the other). Usually, the top element is called the root element (Node 1 is the root element in the figure below).

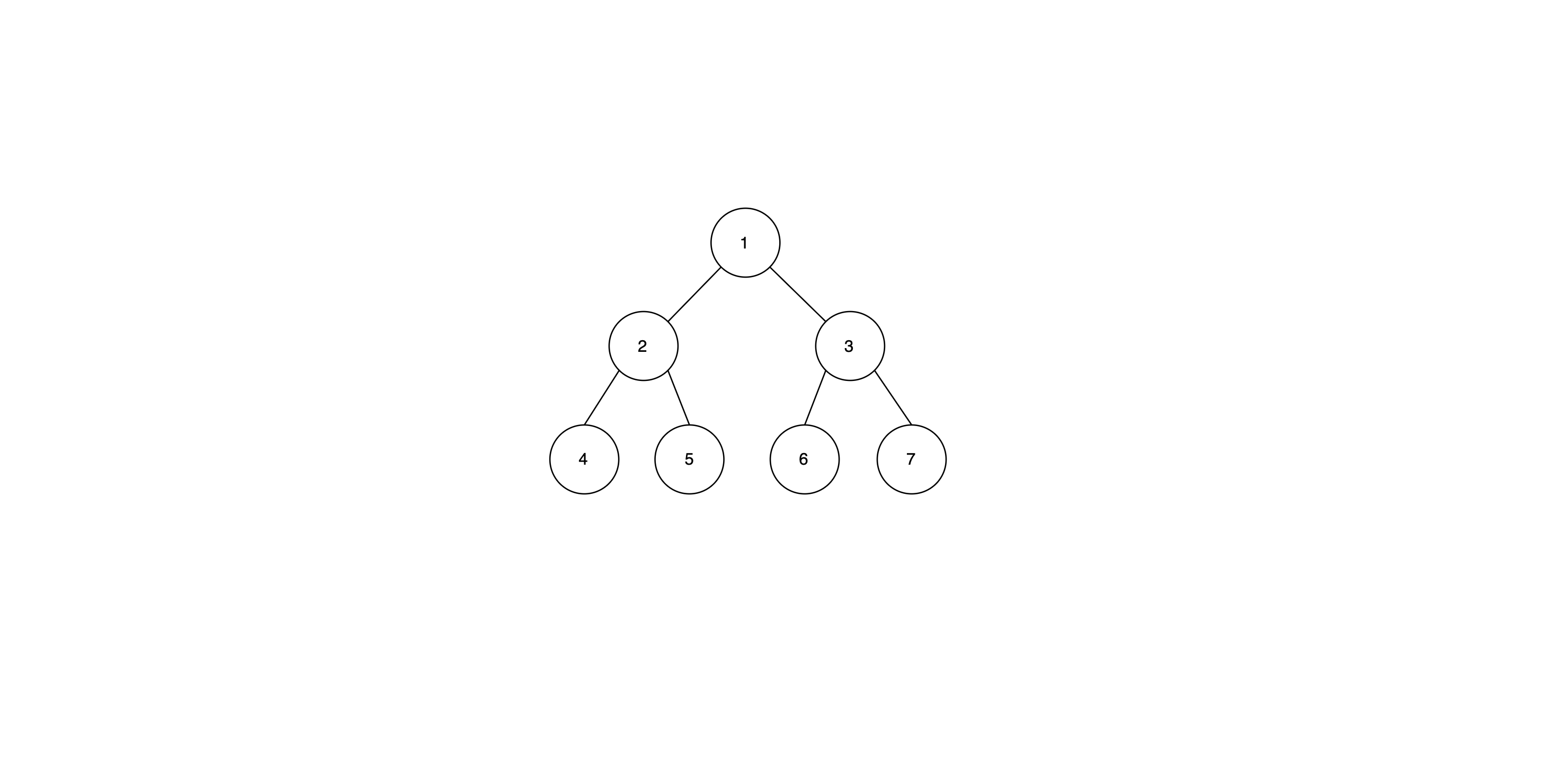
Tree Definition:

For a tree $T$, it is a set of nodes storing elements that have a hierarchical (parent-child) relationship with following rules:

• For a non-empty tree, it has a top node, which is called the root of $T$, and the root node is the only node that has no parent node;
• Expect the root, each node $n$ of $T$ has a unique parent node $p$, each node with parent node $p$ is the child node of $p$;
• A tree with zero node is empty;

---

1.2 Tree Properties

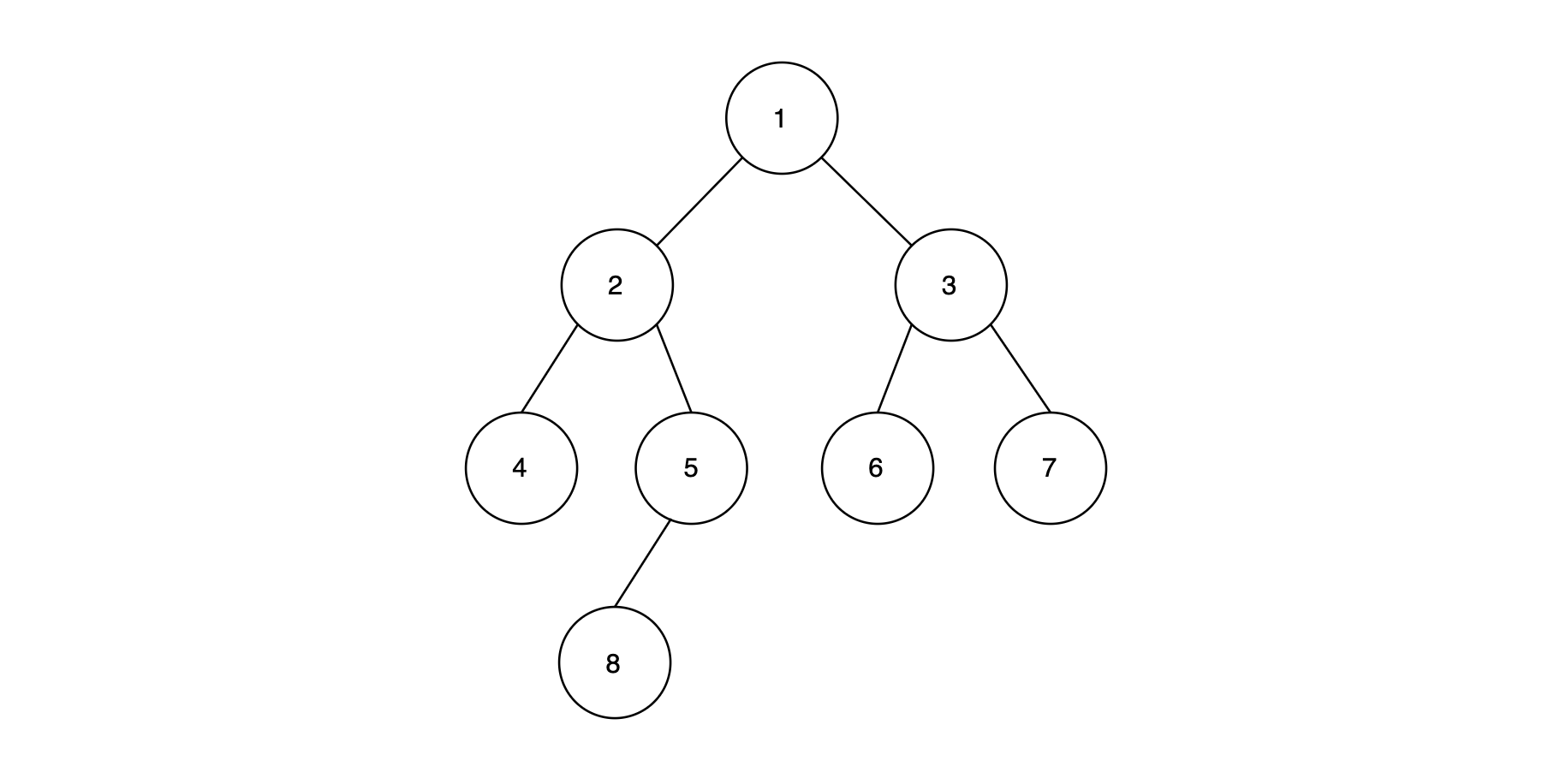
Node Relationships:

• siblings: If two nodes have the same parent node, they are siblings;
  • (Node 2 and Node 3, Node 4 and Node 5, Node 6 and Node 7 are siblings);
• external: A node is external if it has no child node, which is also called a leaf;
  • (Node 4, 6, 7 and 8 are external, leaves);
• internal: A node is internal if it has at least one child node;
  • (Node 1, 2, 3 and 5 are internal);
• ancestor: A node $a$ is the ancestor of a node $b$ if $a=b$ or $a$ is the ancestor of the parent of $b$, which means $a$ is the ancestor of all node connected below $a$.
  • (Node 2 is the ancestor of Node 8);
• descendant: A node $b$ is the descendant of a node $a$ if $a$ is the ancestor of a node $b$, which means that all node connected below $a$ are the descendent of $a$.
  • (Node 8 is the descendant of Node 1);
• subtree: A subtree of a tree $T$ rooted at node $n$ is the tree contains all descendants of $n$ including $n$ itself;
  • (A tree with Node 3, 6 and 7 rooted at Node 3 is the subtree of this Tree);

Edges and Paths:

• edge: The pair of node $(a,b)$, where $a$ is the parent node of $b$;
  • (pair of Node 1 and Node 2 is the edge of Tree);
• path: The sequence of nodes, where two consecutive nodes are connected by an edge;
  • (Path 1-2-5-8 is a path of Tree);

---

2. Tree ADT

Based on the Position ADT in the previous post, we can build the Tree ADT using the Position representing the Node in tree, and the Position has the parent-child relationship to fulfill the tree definition.

• getElement(): Return the element stored in the node (position);
• root(): Return the root node (position) of the tree, null if the tree is empty;
• parent(p): Return the parent node (position) of the node $p$, null if $p$ is the root node;
• children(p): Return an iterable instance of the children nodes (position) of the node $p$, null if $p$ has no child node;
• numChildren(p): Return the number of children of the node $p$;
• isInternal(p): Return true if $p$ is an internal node;
• isExternal(p): Return true if $p$ is an external node;
• isRoot(p): Return true if $p$ is the root node;
• size(): Return the number of nodes (positions or elements) in the tree;
• isEmpty(): Return true if the tree is empty (no nodes, no positions);
• iterator(): Return an iterator of the elements in the tree;
• positions(): Return an iterable instance of the positions (nodes) in the tree;

---

2.1 Tree Interface in Java

public interface Tree<E> extends Iterable<E> {
    Position<E> root();
    Position<E> parent(Position<E> p) throws IllegalArgumentException;
    Iterable<Position<E>> children(Position<E> p) throws IllegalArgumentException;
    int numChildren(Position<E> p) throws IllegalArgumentException;
    boolean isInternal(Position<E> p) throws IllegalArgumentException;
    boolean isExternal(Position<E> p) throws IllegalArgumentException;
    boolean isRoot(Position<E> p) throws IllegalArgumentException;
    int size();
    boolean isEmpty();
    Iterator<E> iterator();
    Iterable<Position<E>> positions();
}

---

3. Abstract Tree Base Class

Abstract class may contain some concrete methods, as well as leave some method body empty.

Ths main purpose of the abstract class is to be the base class. Because it has some concrete methods, which may be used on some common functions, so less work is needed when implementing the abstract class through inheritance.

The Tree Interface is now leaving all methods body empty, which hides all low-level implementation details. However, there are some trivial methods that can be implemented without knowing the details of the other low-level implementation.

Therefore we can build a AbstractTree base class as a abstract class, and implement the trivial methods of Tree, which are isInternal(p), isExternal(p), isRoot(p), and isEmpty(). Thus, once a concrete class derives from AbstractTree, as well as implement the rest of the methods, all methods are implemented.

Java Implementation:

public abstract class AbstractTree<E> implements Tree<E> {
    public boolean isInternal(Position<E> p) throws IllegalArgumentException {
        return  numChildren(p) > 0;
    }
    public boolean isExternal(Position<E> p) throws IllegalArgumentException {
        return numChildren(p) == 0;
    }
    public boolean isRoot(Position<E> p) throws IllegalArgumentException {
        return p == root();
    }
    public boolean isEmpty() {
        return size() == 0;
    }
}

---

4. Depth of Tree

The depth of the node $p$ is the number of ancestor of node $p$, expect itself. (Thus, the depth of the root node is 0.)

Recursively Definition of Depth of node $p$:

• If $p$ is the root node, the depth of $p$ is 0;
• Or, the depth of $p$ is one plus the depth of its parent node.

Java Implementation:

public int depth(Position<E> p) {
    if (isRoot(p)) {
        return 0;
    }
    return 1 + depth(parent(p));
}

Running time: $O(d_p+1)$, where $d_p$ is the depth of node $p$.
Worst-case running time: $O(n)$, where $n$ is the number of nodes in the tree.

---

5. Height of Tree

The height of tree is the maximum of the depths of all nodes (positions) in the tree, where the node with maximum depth must be a leaf.

Intuitive Implementation in Java:

public int heightBad() {
    int h = 0;
    for (Position<E> p : positions()) {
        if (isExternal(p)) {
            h = Math.max(h, depth(p));
        }
    }
    return h;
}

However, this approach is not efficient for traversing all leave node in the Tree.

The running time is $O(n+\sum_{p \in L}(d_p+1))$, where $L$ is the set of all leaf nodes.
The worst-case running time is $O(n^2)$, where $n$ is the number of nodes in the tree.

---

The more efficient way is implementing in a recursive way as the tree is defined recursively.

To find the height of a node $p$:

• If $p$ is a leaf, its heigh is 0;
• Or, the height of $p$ is one plus the maximum of the heights of its children.

To calculate the height of Tree, we only need to get the height of its root through above recursive way.

Java Implementation:

public int height(Position<E> p) {
    int h = 0; // Default height of a leaf is 0
    // leaf nodes will skip the loop for no children
    for (Position<E> c : children(p)) {
        h = 1 + Math.max(h, height(c));
    }
    return h;
}

// calculate the height of the tree by passing root node as parameter
int treeHeight = height(root());

The running time is $O(c_p+1)$, where $c_p$ is the number of children of node $p$.
When calculate the height of the tree, the worst-case running time is $O(n)$, where $n$ is the number of nodes in the tree.

---

6. Time for Binary Tree

In the previous posts, we have discussed about the general linear data structure - List, as well as important concept of Position.

And in the last post, we have introduced the iterator and its applications, which is powerful for traversing process.

In this sharing post, we studied the basis concept of general tree based on the abovementioned Position ADT and iterator.

Next, with all background knowledge, we are able to discuss about a much more important tree data structure - Binary Tree. See you next time!

---

References

Goodrich, M., Tamassia, R., & O’reilly, A. (2014). Data Structures and Algorithms in Java, 6th Edition. John Wiley & Sons.

---

写在最后

Tree 相关的知识会继续学习，继续更新.
最后，希望大家一起交流，分享，指出问题，谢谢！

---

原创文章，转载请标明出处
Made by Mike_Zhang

感谢你的支持