多米诺配对问题 Domino Matching with Python

Made by Mike_Zhang

数据结构与算法主题：

1. Preview

Domino Matching(多米诺配对) 问题来自于我的一门名为 Computational Thinking and Problem Solving (计算思维和问题解决 ) 的课，主要培养我们的计算思维。


多米诺骨牌 Dominos

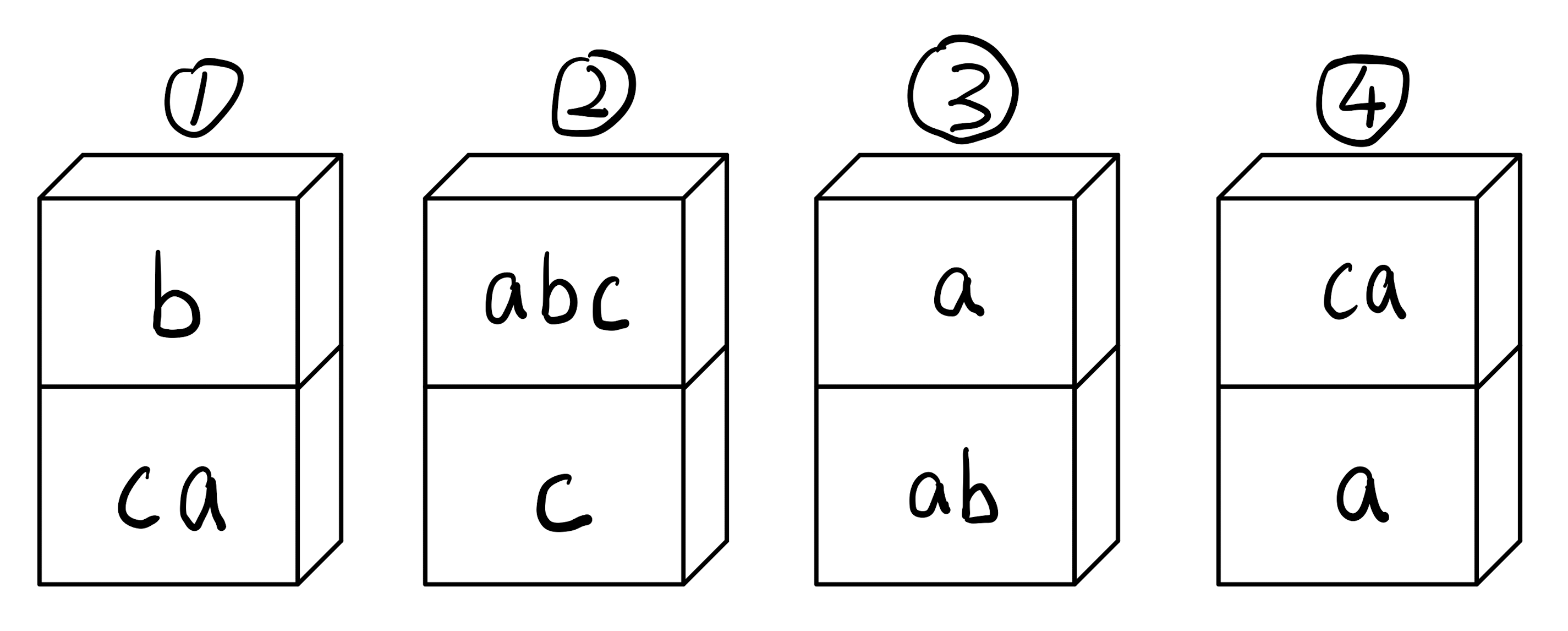
情景：

如上图所示，有四块多米诺骨牌（1～4），每块都有上和下两部分组成，上下两部分的成分是相同的（同为字母、同为数字…），每块多米诺骨牌都存在无数块。

问题：

从提供的一组多米诺骨牌（如上图中的4块）中选取多米诺骨牌，并将它们水平（如麻将般）组合起来，可重复选取，要求最后的组合体的上面部分和下面部分相同。问，此组多米诺骨牌能否组成要求的组合体，若能，组合的顺序如何？

示例：


多米诺骨牌配对体 Matched Domino

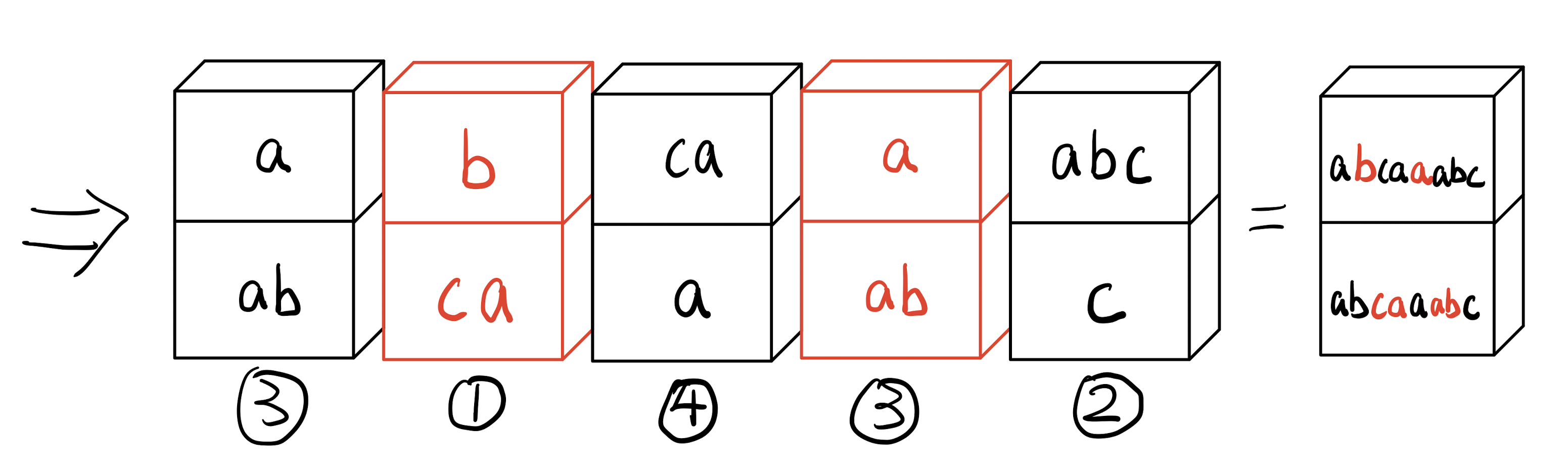
示例：


多米诺骨牌配对体 Matched Domino

2. Computational Thinking

我们可能会对每一种组合进行尝试，但在此过程中会有一些影响组合决定的条件。

2.1 Two Conditions

当尝试把下一个多米诺骨牌连接到现有的组合体时，即将产生的新组合体会有两个检查条件：

  1. 其是否为完全配对体(Matched Domino)，也就是最后我们希望得到的配对体。
  2. 其是否为部分配对体(Partially Matched Domino)，检查将其添加到组合体后，此时的组合体能否有成为配对体的可能。

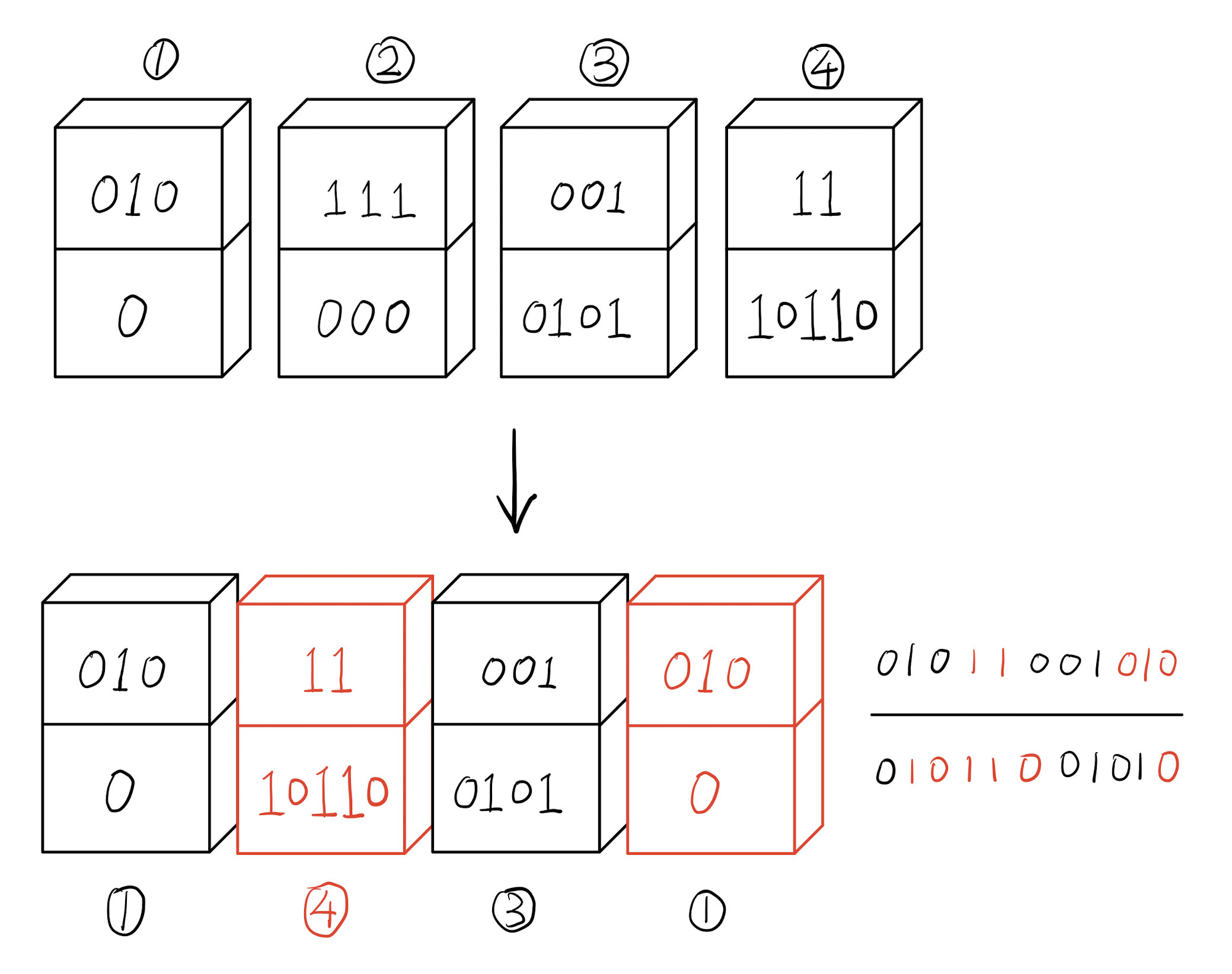
例如：


完全配对体 Matched Domino

部分配对体 Partially Matched Domino

非部分配对体 Non-Partially Matched Domino
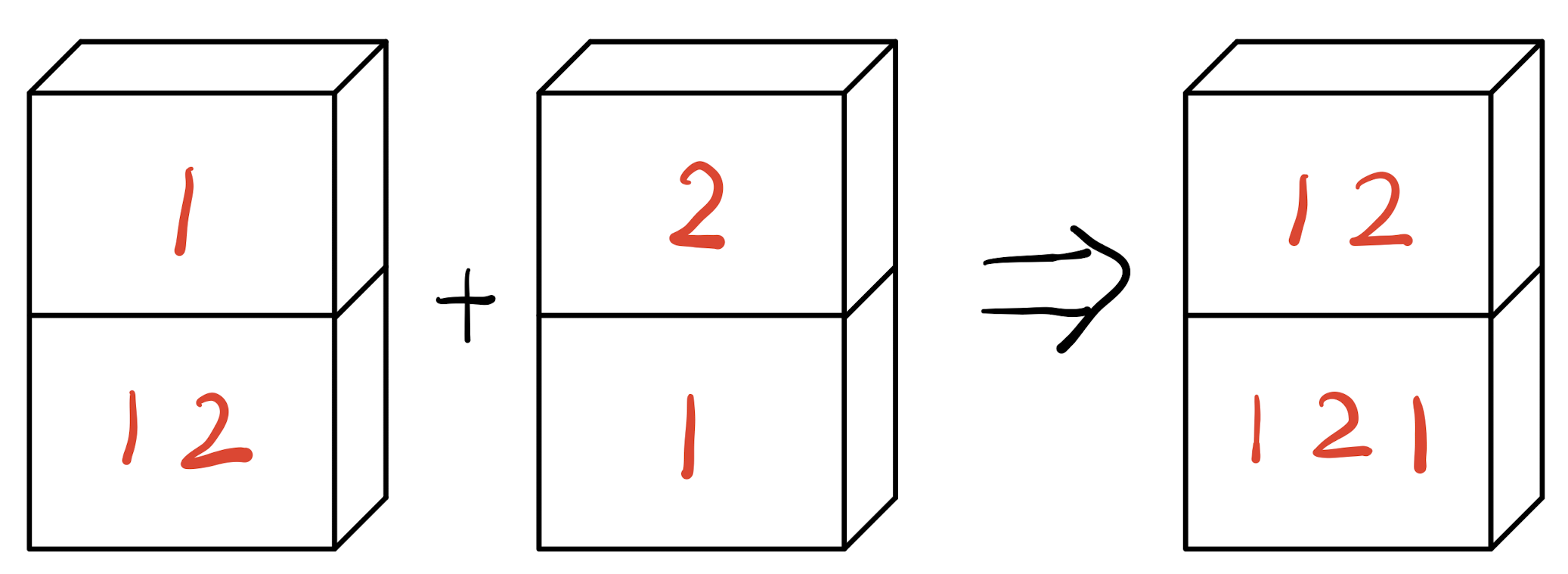
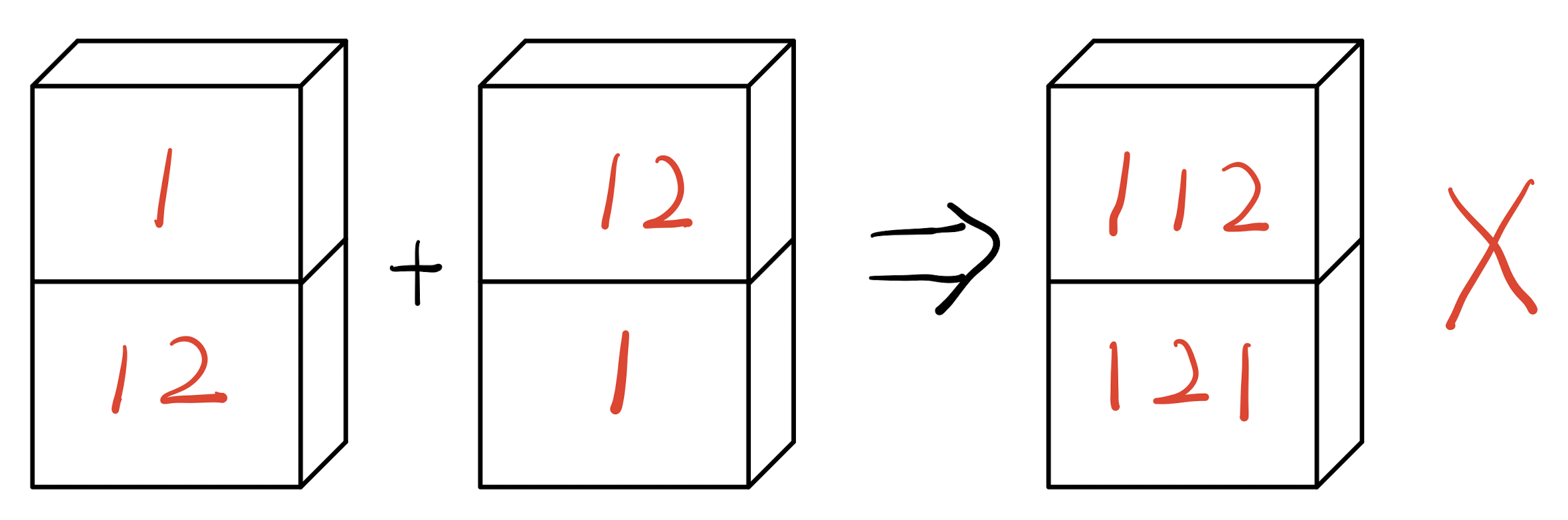
(非完全配对体 Non-Matched Domino)

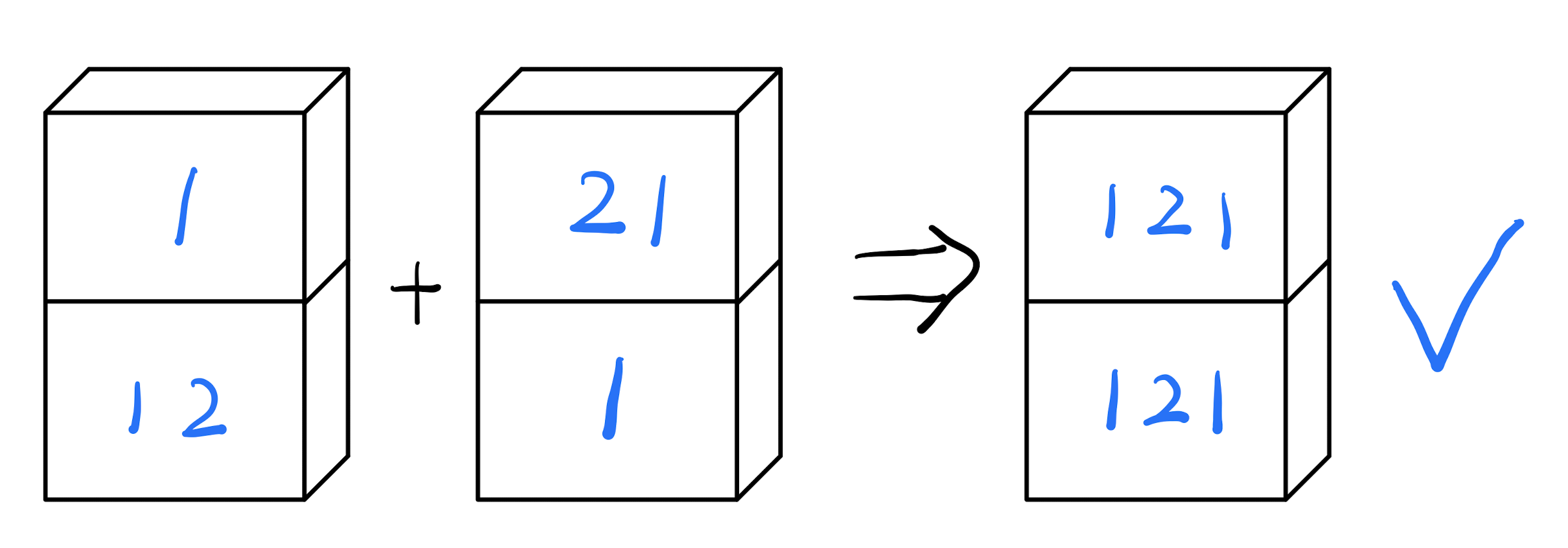
在第一个例子中，若将[21,1]多米诺骨牌连接到原有组合体后，使原有组合体变成完全配对体 (Matched Domino)，因此[21,1]多米诺骨牌为下一个连接的选择，并且其为最后一块多米诺骨牌。

在第二个例子中，若将[2,1]多米诺骨牌连接到原有组合体后，会使原有组合体变成部分配对体 (Partially Matched Domino)，因此[2,1]多米诺骨牌可以作为下一个连接的选择。

在第三个例子中，若将[12,1]多米诺骨牌连接到原有组合体后，会使原有组合体变成非部分配对体 (Non-Partially Matched Domino)，因此[12,1]多米诺骨牌不能作为下一个连接的选择。

通过这两个检查条件，可以判断哪些多米诺骨牌可以成为下一个连接的选择。

2.2 Starting Domino

万事开头难。
上面明确了选择多米诺骨牌的中间过程，但是还需要确定第一块多米诺骨牌的选择。

可以明确的是，最后的组合体上下两部分一定是相同的。因此，第一块多米诺骨牌的上下两部分肯定是部分相同的。也就是说第一块多米诺骨牌的“组合体”肯定是部分配对体 (Partially Matched Domino)。

例如：


多米诺骨牌 Dominos

上图所示的一组多米诺骨牌中，只有3号是部分配对体 (Partially Matched Domino)，因此只有其可以作为第一块多米诺骨牌。


多米诺骨牌 Dominos

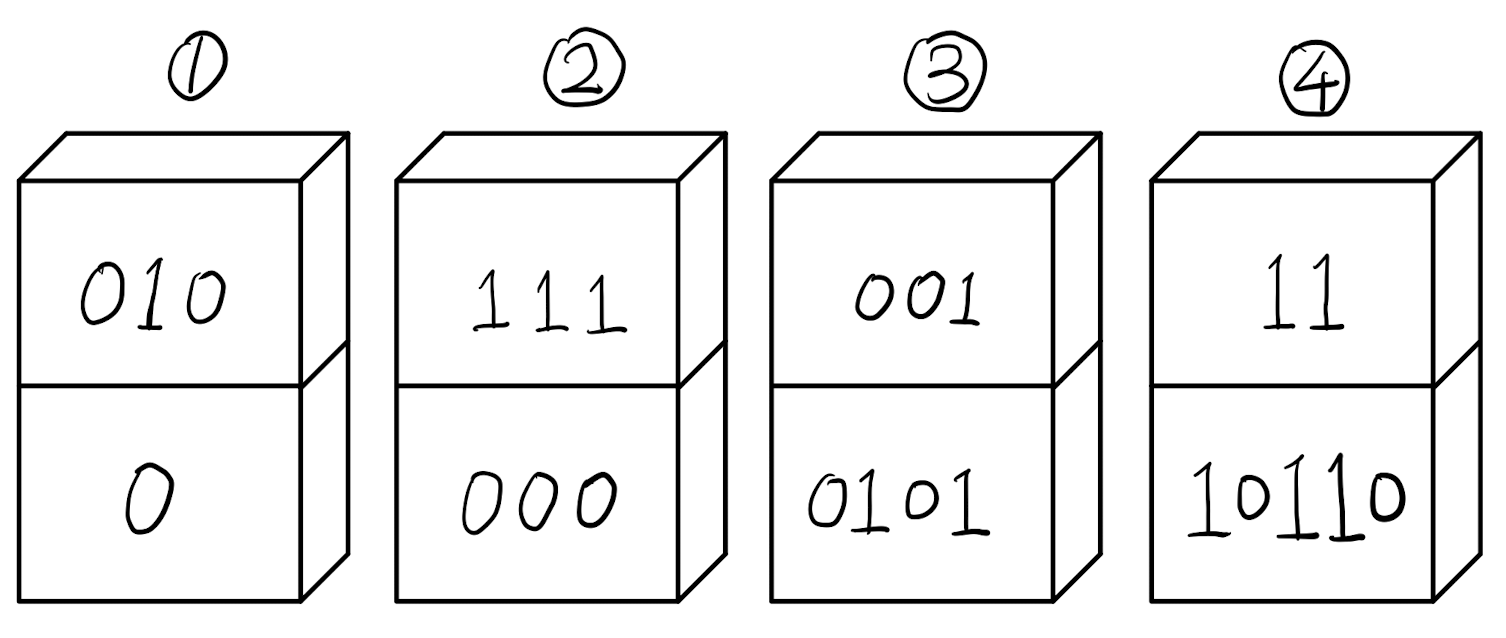
上图所示的一组多米诺骨牌中，只有1号是部分配对体 (Partially Matched Domino)，因此只有其可以作为第一块多米诺骨牌。

4.3 Process

根据以上思考，可以产生对此问题的处理步骤：

  1. 找到第一块多米诺骨牌；
  2. 若找不到能作为第一块的多米诺骨牌，则这一组多米诺骨牌不能组成组合体，程序结束；
  3. 向现有组合体连接任意一块多米诺骨牌；
  4. 若其可以组成完全配对体 (Matched Domino)，则完成配对，得到最后的组合体，程序结束；
  5. 若其可以组成部分配对体 (Partially Matched Domino)，则重复步骤2；
  6. 若其可以组成非部分配对体 (Non-Partially Matched Domino)，则将其移出现有组合体，并重复步骤2，尝试不同的多米诺骨牌；
  7. 若任何一块多米诺骨牌都不能连接到第一块多米诺骨牌后，则程序结束。

3. Problem Solving with Python Code

以下为多米诺配对问题 (Domino Matching) 的 Python 解决方法。

代码链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
# Made by Mike_Zhang
# Domino Matching
def isMatchedDomino(inDomino):
    """
    function to check whether this Domino is matched

    parameter:
        - inDomino: Domino to check
    return:
        - True: it is matched
        - False : it is NOT matched
    """
    upperList = []
    lowerList = []
    for d in inDomino:
        upperList.append(d[0])
        lowerList.append(d[1])
    upper = "".join(upperList)
    lower = "".join(lowerList)
    if (len(upper)==len(lower)):
        if (upper == lower):
            return True
        else:
            return False
    return False


def isPartialMatched(inDomino):
    """
    function to check whether a part of this Domino is matched, part refers to the longest part of a Domino having same lenth of upper half and lower half part
    e.g., [["a","ab"],["b","ca"]] is Partially Matched, [["a","ab"],["b","ca"],["ca","a"],["abc","c"]] is NOT Partially Matched

    parameter:
        - inDomino: Domino to check
    
    return: 
        - mark:
            - True: Partially Matched
            - False: NOT Partially Matched
    """
    upperList = []
    lowerList = []
    for d in inDomino:
        upperList.append(d[0])
        lowerList.append(d[1])
    upper = "".join(upperList)
    lower = "".join(lowerList)
    i = min(len(upper),len(lower))-1
    mark = True
    while(mark == True and i >= 0):
        if (upper[i] != lower[i]):
            mark = False
        i=i-1
    return mark


def getStartDominoList(inDominoList):
    """
    function to get a list of Dominos that each one is partially matched Domino
    e.g. getStartDominoList([["010","0"],["111","000"],["001","0101"],["11","10110"]]) = [["010","0"]]
    getStartDominoList([["b","ca"],["abc","c"],["a","ab"],["ca","a"]]) = [["a","ab"]]
    
    the first Domino in a matched Domino must be selected from that list of Dominos

    parameter:
        - inDominoList: a list of Dominos to check
    return:
        - a list of required Dominos
    """
    resultList = []
    for d in inDominoList:
        if (isPartialMatched([d])):
            resultList.append(d)
    return resultList


def isNextDominoValid(inDomino,inNext,Dominos):
    """
    the CORE function 
    to recursively check whether next Domino can generate a matched Domino after appending to the original Domino,
    and finally modify the original Domino to a matched Domino, if can generate.

    parameter:
        - inDomino: the original Domino
        - inNext: the next Domino 
        - Dominos: all given Dominos
    return:
        - flag: 
            - True: can generate a matched Domino
            - False: can NOT generate a matched Domino
    """
    flag = False
    inDomino.append(inNext)
    if (isMatchedDomino(inDomino) == True):
        flag = True
    elif (isPartialMatched(inDomino) == False):
        flag = False
        inDomino.pop()
    else:
        for d in Dominos:
            if (isNextDominoValid(inDomino,d,Dominos)):
                flag = True
                break
    return flag


def main():
    Dominos = [["b","ca"],["abc","c"],["a","ab"],["ca","a"]]
    #Dominos = [["010","0"],["111","000"],["001","0101"],["11","10110"]]
    #Dominos = [["001","00"],["0","100"]]

    flag = False
    resultDominos = list()
    startDominoList = getStartDominoList(Dominos)

    if (len(startDominoList) == 0):
        flag = False
    else:
        for startDomino in startDominoList:
            tmpList = list()
            tmpList.append(startDomino)
            for d in Dominos:
                if (isNextDominoValid(tmpList,d,Dominos)):
                    resultDominos = tmpList
                    flag = True
                    break
    if (flag == True):
        print("Yes, exist a solution:")
        print(resultDominos)
    else:
        print("No, not exist any solutions")

main()
# Domino Matching
# Made by Mike_Zhang

写在最后

解决多米诺配对问题的方法有很多种，我的方法并非最优解，欢迎大家尝试。
最后，希望大家一起交流，分享，指出问题，谢谢！

原创文章，转载请标明出处
Made by Mike_Zhang




感谢你的支持
Data Structure and Algorithm > Algorithm
#Python #Domino Matching
多米诺配对问题 Domino Matching with Python
https://ultrafish.io/post/domino-matching/
Author
Mike_Zhang
Posted on
November 4, 2021
Licensed under