Disjoint Set Introduction - 并查集简介

Made by Mike_Zhang

数据结构与算法主题：

本文记录并查集(Disjoint Set)的学习，包括Graph的简介，Union和Find的实现，以及其的优化。

1 Introduction of Graph

1.1 Undirected Graph

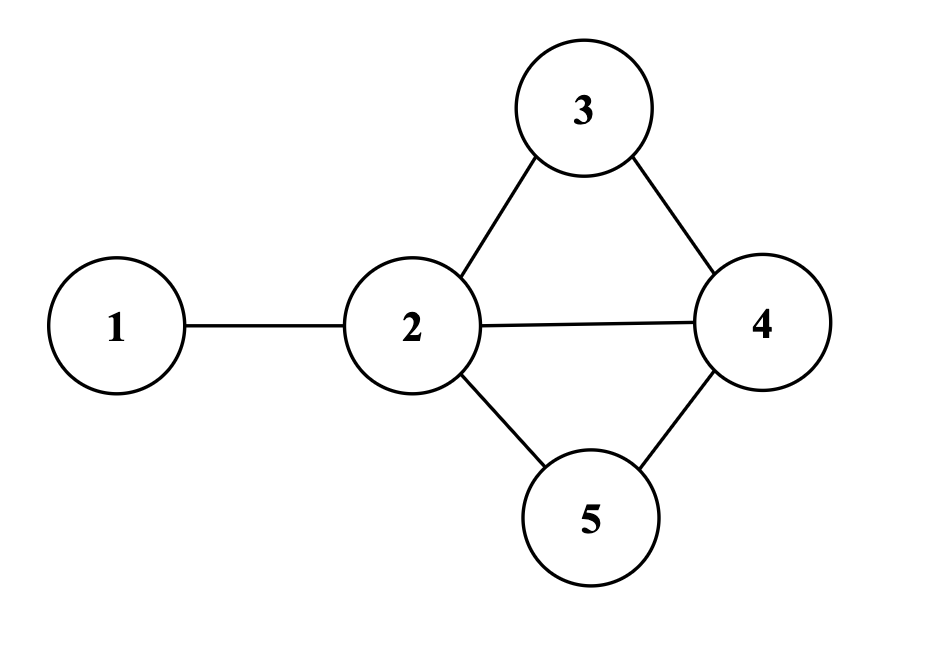
Undirected Graph

Graph $G=(V,E)$

$V=$ the set of all vertices (nodes);
$E=$ edges (arcs) between pairs of vertices.

Undirected Graph: each edge do NOT have direction, having a two-way relation.

1.2 Directed Graph

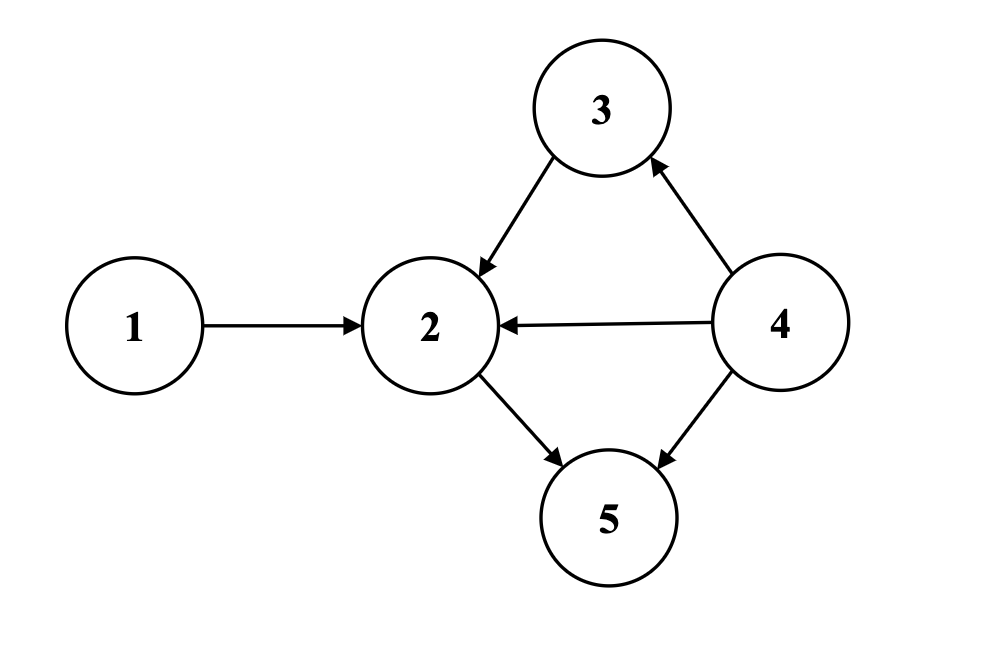
Directed Graph

Directed Graph: every edges are directional.

1.3 Weighted Graph

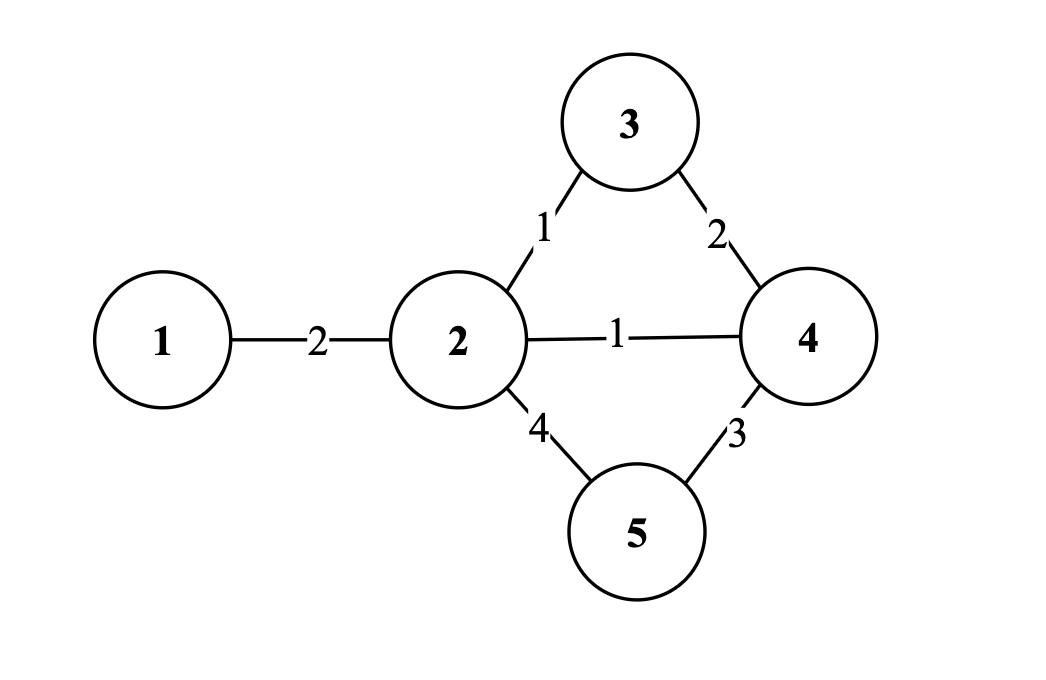
Weighted Graph

Weighted Graph: each edge has an associated weight.

1.4 Terminologies

Vertex: The node of a graph;
Edge: The connection between two vertices;
Path: The sequence of vertices from one vertex to another;
Path Length: The number of edges in a path;
Cycle: A path with same starting vertex and endpoint vertex;
Connectivity: Two vertices are connected if there exists at least one path between them;
Degree of a Vertex: The number of edges connecting the vertex in a unweighted graph;
In-Degree: For weighted graph, the number of edges incident to a vertex, In-degree of vertex 2 is 3;
Out-Degree: For weighted graph, the number of edges incident from a vertex, In-degree of vertex 2 is 1;

2 Disjoint Set

2.1 Introduction

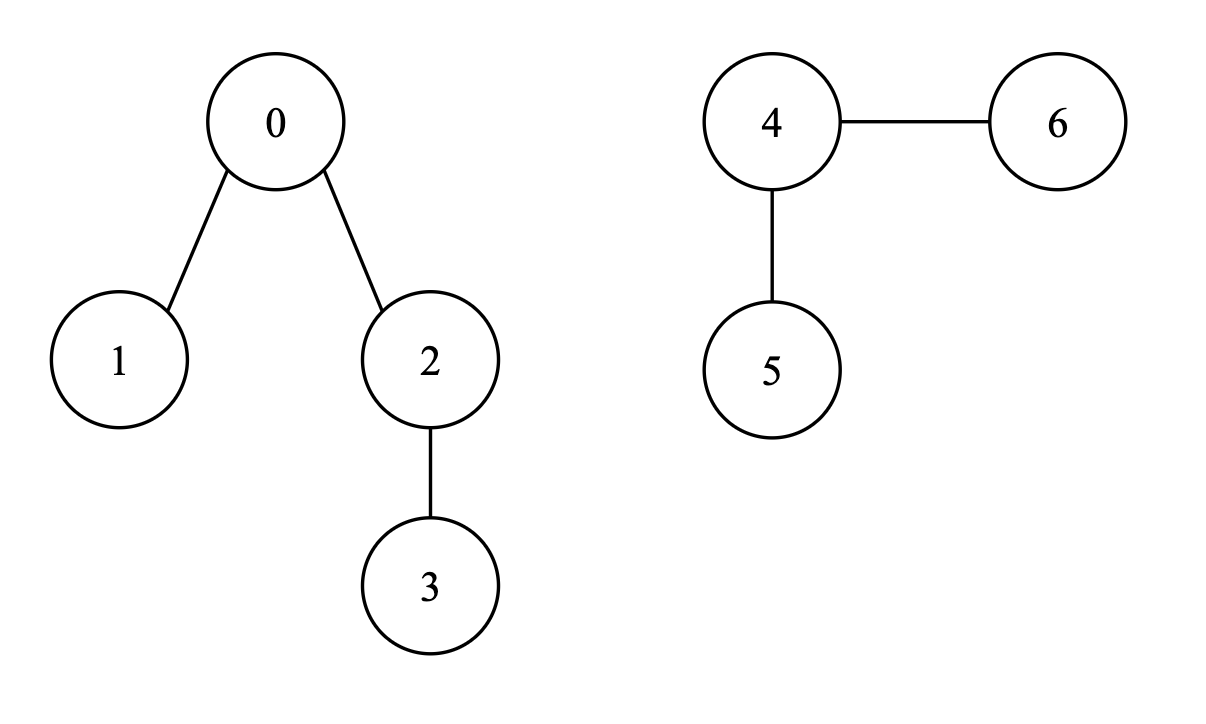
Graph

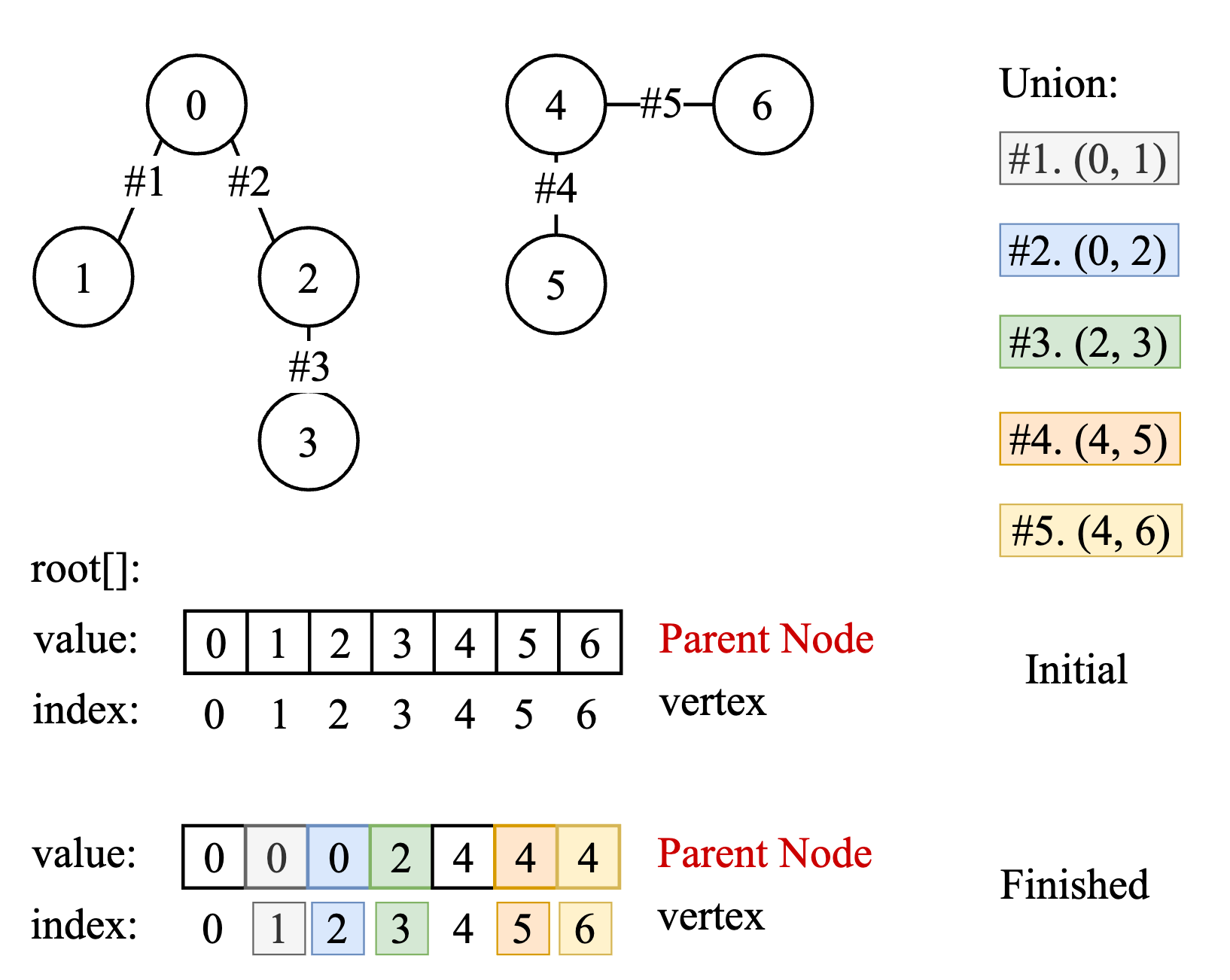
In graph, Disjoint set (并查集) can help us quickly check (Find) whether given two vertices is connected or not, e.g., vertex 1,3 are connected for there is a path 1-0-2-3, vertex 3,5 is not connected for there is no path from 3 to 5. It also can help us union two disjoint set into a set and maintain their relationship.

The main point for the disjoint set function is to check whether two vertices have a same parent root vertex, if yes, then there are connected, e.g. root vertex of 1 and 3 is vertex 0, so they are connected, and the root vertex of 3 is 0, root vertex of 5 is 4, so having different root means 3 and 5 are not connected.

2.1.1 Basic Disjoint Set Implementation:

  • Union function to add node into the disjoint set.

A root array, each index represent each vertex; the value of each element refers to vertex’s parent

Basic Disjoint Set Implementation - Union
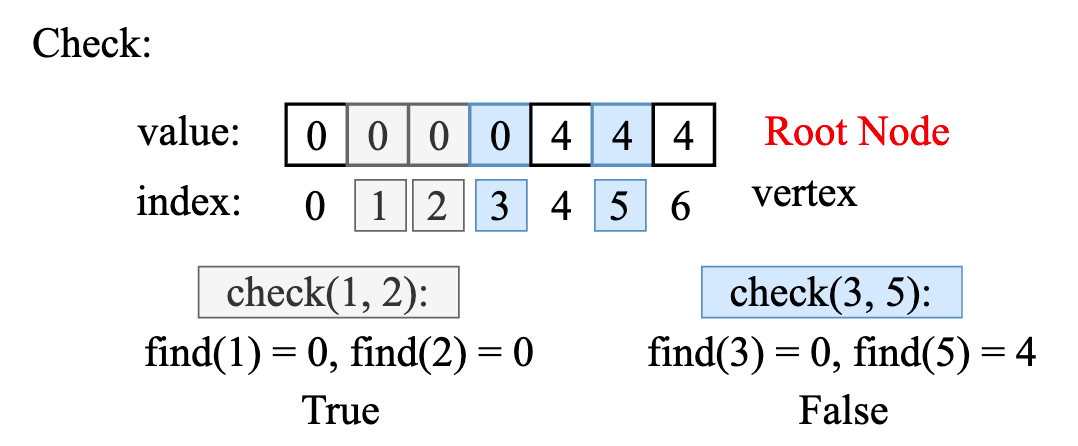
  • check function, using find function to find the parent of the vertex until the parent of the vertex is itself means the root is found, then compare whether their root is same or not, same means connected.
Basic Disjoint Set Implementation - Find

2.2 Quick Find

Disjoint Set has two main function- Union and Find;

Quick Find is a optimization of Find function of generic disjoint set by storing the root node of vertices in the root array.

Advantage:
It directly stores the root node of a vertex in the root array instead of the parent node, which makes the Find function become access the value of the index in the array, making the Find function much faster.

Drawback:
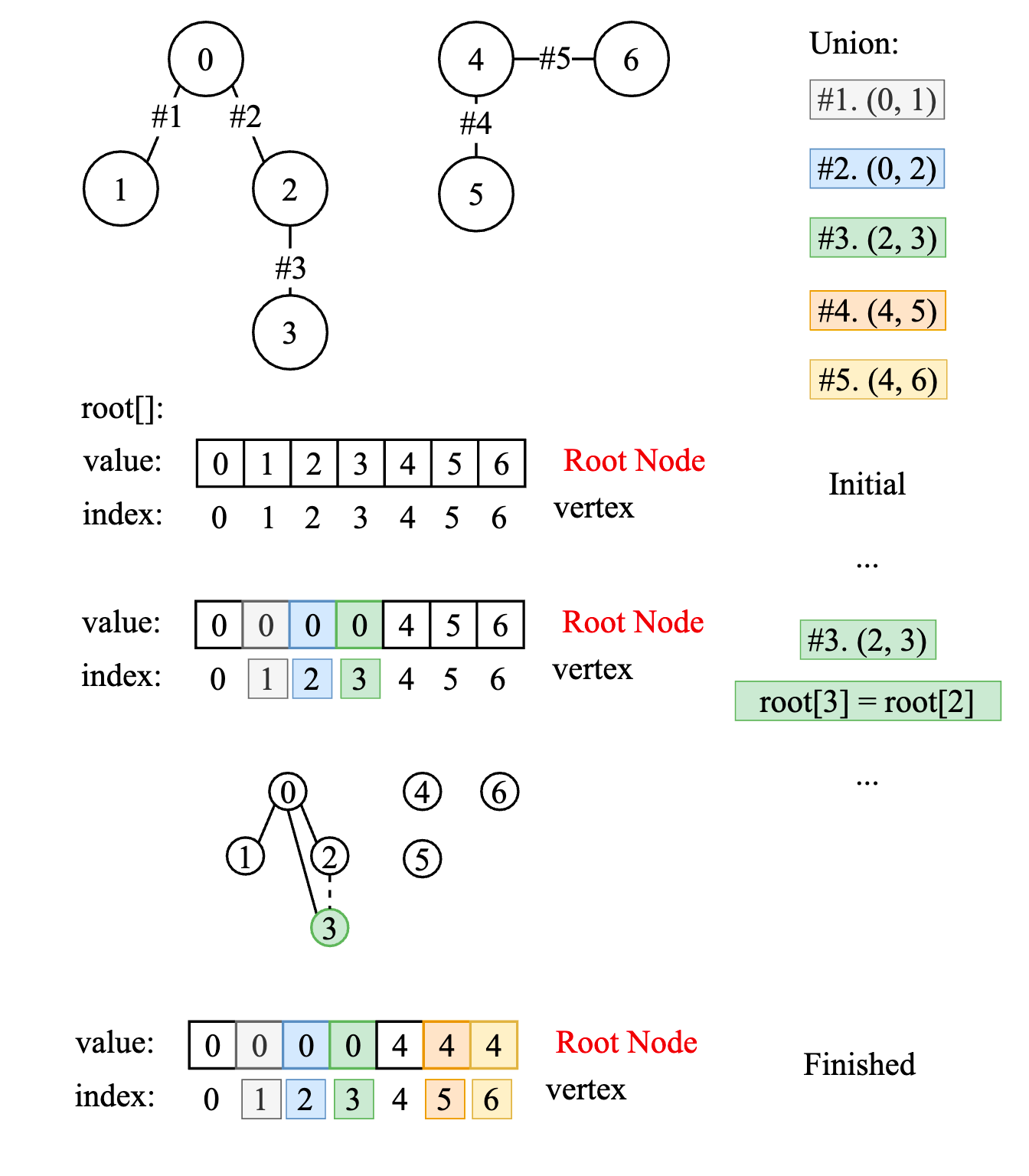
But it slows down the Union function, because the root array stores root(s) of each node in the disjoint set, every Union function needs to update a specific root, which is found by traversing the entire set. For Union(A,B), we have to every node has a same root as root(B), and then update them to root(A)

Directly stores the root node of a vertex in the root array:

Quick Find

Faster finding, just access the value at the index:

Quick Find

Slow down the union function, for entire set traversing, especially union a big set:

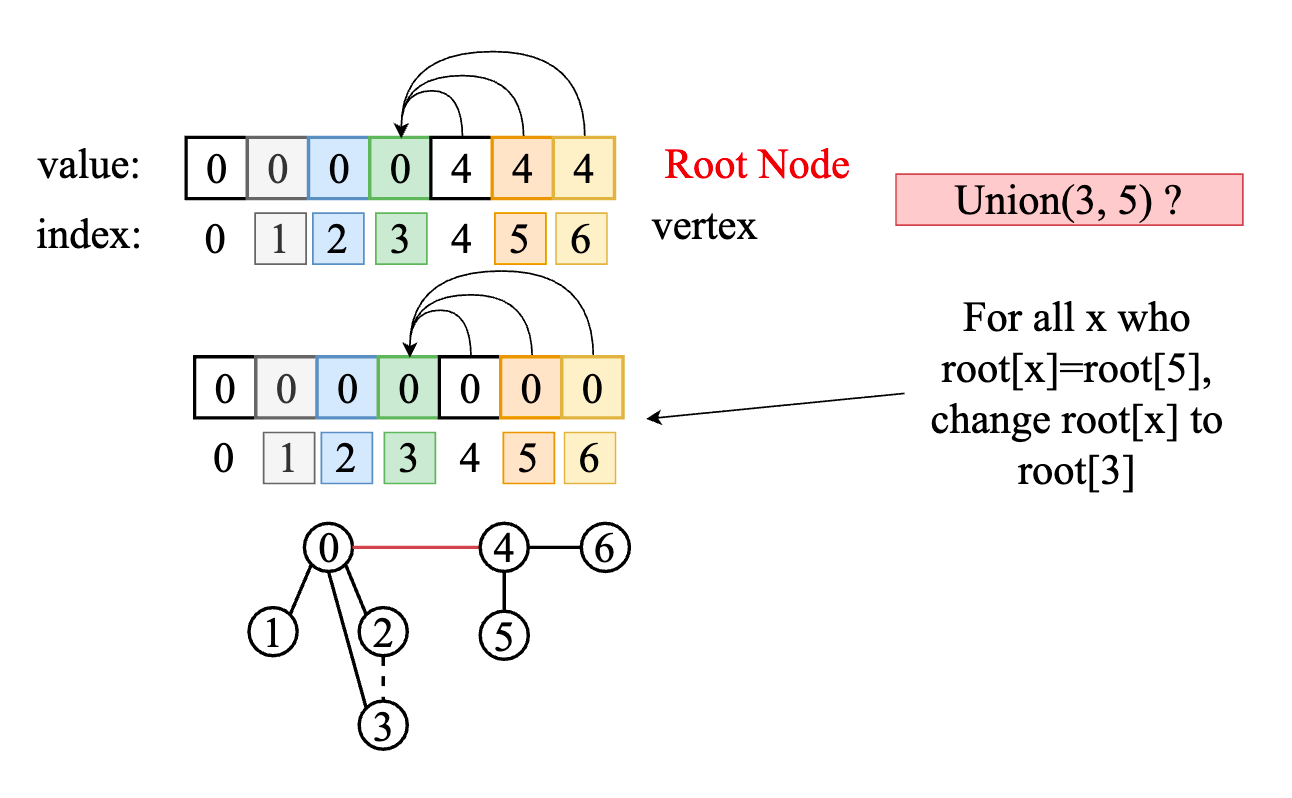
Quick Find

Java implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class QuickFind {
    private int[] root;

    public QuickFind(int size) {
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    public int find(int x) { // Directly stores the root node
        return root[x]; // return the value of index as the root
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            for (int i = 0; i < root.length; i++) { // Traversing entire set
                if (root[i] == rootY) { // Who has the same root as y,
                    root[i] = rootX; // change its root to root of x
                }
            }
        }
    }

    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }

    public String getRootArr(){
        StringBuilder sb = new StringBuilder();
        for (int i:root) {
            sb.append(Integer.toString(i));
        }
        return sb.toString();
    }
}

Run the test code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Main {
        public static void main(String[] args) {
            QuickFind qf = new QuickFind(7);

            qf.union(0, 1);
            qf.union(0, 2);
            qf.union(2, 3);
            qf.union(4, 5);
            qf.union(4, 6);

            System.out.println(qf.isConnected(1, 3)); 
            System.out.println(qf.isConnected(1, 5)); 
            System.out.println(qf.getRootArr().toString()); 

            uf.union(3, 5);
            System.out.println(qf.isConnected(1, 5));
            System.out.println(qf.getRootArr().toString());
        }
}

Output:

1
2
3
4
5
true
false
0000444
true
0000000

Time Complexity:

find(): $O(1)$, for accessing an element of the array at the given index.
union(): $O(N)$, for traversing the entire array.

2.3 Quick Union

Quick Union is actually the Basic Disjoint Set Implementation abovementioned, which optimizes the Union function compared with Quick Find. It store the parent root in the root array instead of the root node.

Advantage:
When union(A, B), only change the root of root of B to the root of A, then A and B will be connected, i.e. root[find[A]] = find[B]. No need to traverse the entire set like Quick Find, because we only store the parent node in the array, mean to be having less modify.

Drawback:
Due to the root array only store the parent node, once we want to find the root of a node, we need to look up the parents through the array until find the top root, which means find whose root node is itself, root[A] = A. This process will take some time comparing with just accessing the value of index in Quick Find.

Java implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class QuickUnion {
    private int[] root;

    public QuickUnion(int size) {
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    public int find(int x) { // Store the parent of the vertex
        while (root[x] != x) { // Loop until find the root
            x = root[x];
        }
        return x;
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
           root[rootY] = rootX; // Union just operates the root node
        }
    }

    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }

    public String getRootArr(){
        StringBuilder sb = new StringBuilder();
        for (int i:root) {
            sb.append(Integer.toString(i));
        }
        return sb.toString();
    }
}

Run the test code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Main {
        public static void main(String[] args) {
            QuickUnion qu = new QuickUnion(7);

            qu.union(0, 1);
            qu.union(0, 2);
            qu.union(2, 3);
            qu.union(4, 5);
            qu.union(4, 6);

            System.out.println(qu.isConnected(1, 2)); // true
            System.out.println(qu.isConnected(3, 5)); // false
            System.out.println(qu.getRootArr().toString());

            qu.union(3, 5);
            System.out.println(qu.isConnected(1, 5)); // true
            System.out.println(qu.getRootArr().toString());
        }
}

Output:

1
2
3
4
5
true
false
0000444
true
0000044

Time Complexity:

find(): $\le O(N)$, for the worst case, we have to traverse all vertices to get the root, e.g. all vertices connected in a line
union(): $\le O(N)$, it composites two find() functions, in the worst case, it also takes $O(N)$ time.

Quick Union is more efficient than Quick Find:

In all, for a N-disjoint set,

Quick Find take exactly $N\times O(N)= O(N^2)$ time;
Quick Union take at most $N\times O(N)= O(N^2)$ time.

2.5 Union by Rank - Optimized Union

Abovementioned, Quick Union will take $O(N^2)$ in the worst case when all vertices connected in a line:

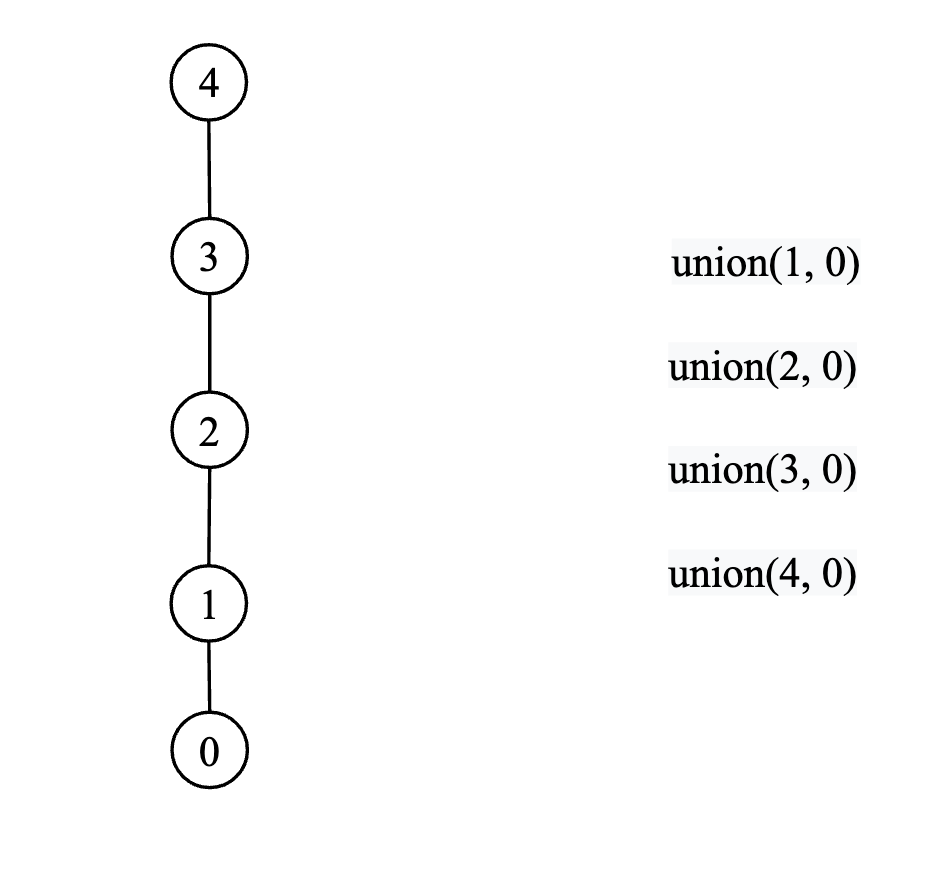
Union by Rank

We can optimize Quick Union by assigning each vertex a rank attribute, which indicate the height of each node, e.g., the height of node 0 is 1, node 4 is 5 in above picture.

When connecting two root node, we choose the root with larger rank as the parent node of another, which can make the rank of each node unchanged. Otherwise, the highest rank will be increased.

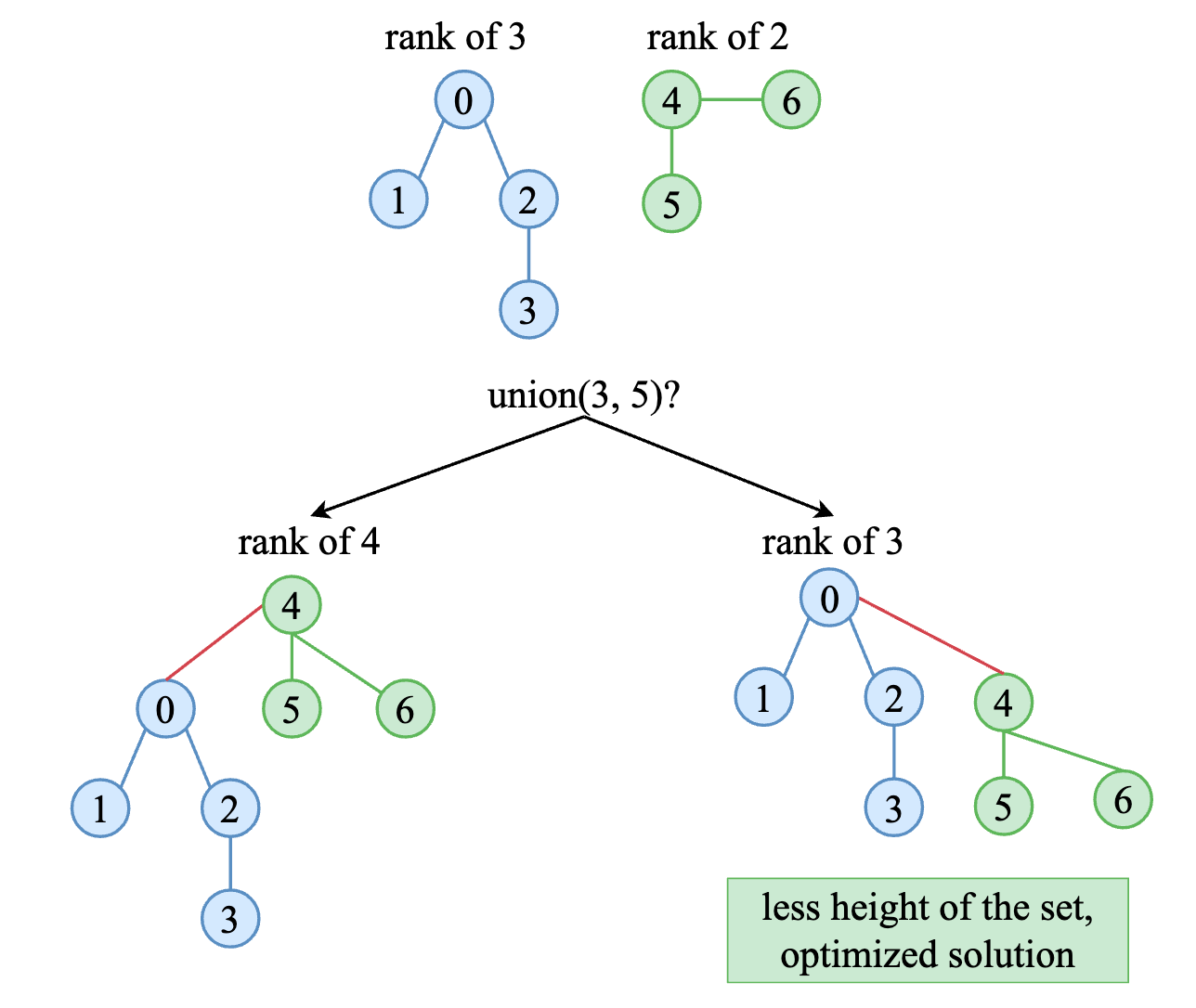
Union by Rank

Java implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class QuickUnion {
    private int[] root;
    private int[] rank; // rank attribute

    public QuickUnion(int size) {
        root = new int[size];
        rank = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
            rank[i] = 1; // initial the rank as 1
        }
    }

    public int find(int x) {
        while (root[x] != x) {
            x = root[x];
        }
        return x;
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            // choose the root with larger rank as parent
            if (rank[rootX] > rank[rootY]) { 
                root[rootY] = rootX;
            } 
            // choose the root with larger rank as parent
            else if (rank[rootX] < rank[rootY]) { 
                root[rootX] = rootY;
            } 
            // if same rank
            else { 
                root[rootY] = rootX; // choose x as parent by default
                rank[rootX] += 1; // increasing the rank of x by 1
            }
        }
    }

    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }

    public String getRootArr(){
        StringBuilder sb = new StringBuilder();
        for (int i:root) {
            sb.append(Integer.toString(i));
        }
        return sb.toString();
    }
}

Test for the worst case:

1
2
3
4
5
6
7
8
9
10
11
12
public class Main {
        public static void main(String[] args) {
            QuickUnion qu = new QuickUnion(5);

            qu.union(1, 0);
            qu.union(2, 0);
            qu.union(3, 0);
            qu.union(4, 0);

            System.out.println(qu.getRootArr().toString());
        }
}

Output:

1
11111

which is:

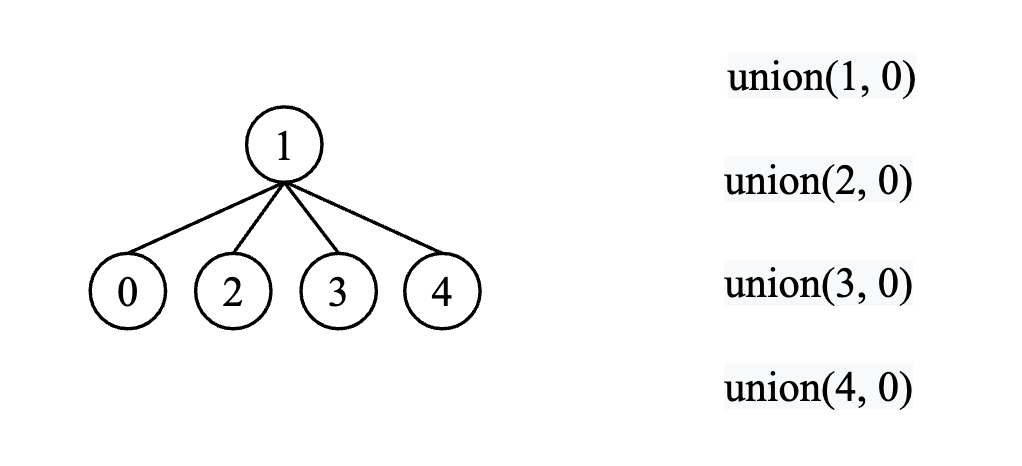
Union by Rank

Time Complexity:

find(): $\le O(\log N)$, for the worst case, we have to traverse all vertices to get the root, e.g. all vertices connected in a line
union(): $\le O(\log N)$, it composites two find() functions, in the worst case, it also takes $O(N)$ time.

2.6 Path Compression - Optimized Find

In the above Quick Union, we find the root of a node by traversing, if we want to find its root again, we have to repeat the traversing again. We can optimize it by Path Compression, which can update the parent node of each traversed one to the finally found root node, then when we find the root again, the root has already been stored in the array, saving a lot of time. This optimization can be done with recursion.

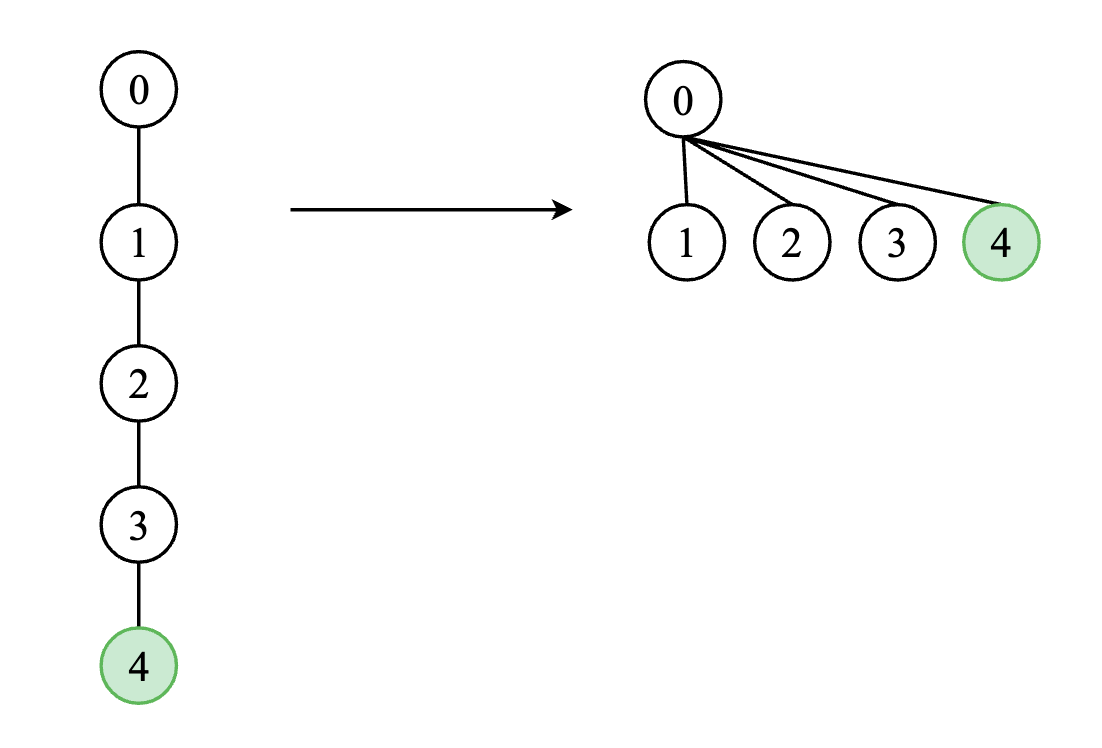
Path Compression

Java implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class QuickUnion {
    private int[] root;

    public QuickUnion(int size) {
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    public int find(int x) {
        if (root[x] == x) {
            return x;
        }
        // Recursively updating each traversed node
        return root[x] = find(root[x]); 
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
           root[rootY] = rootX;
        }
    }

    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }

    public String getRootArr(){
        StringBuilder sb = new StringBuilder();
        for (int i:root) {
            sb.append(Integer.toString(i));
        }
        return sb.toString();
    }
}

Test for the worst case:

1
2
3
4
5
6
7
8
9
10
11
12
public class Main {
        public static void main(String[] args) {
            QuickUnion qu = new QuickUnion(5);

            qu.union(0, 1);
            qu.union(1, 2);
            qu.union(2, 3);
            qu.union(3, 4);

            System.out.println(qu.getRootArr().toString());
        }
}

Output:

1
00000

Time Complexity:

find(): $O(\log N)$ on average;
union(): $O(\log N)$ on average.

2.7 Optimized Disjoint Set

Implement Disjoint set with optimization of both Union by Rank and Path Compression.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class QuickUnion {
    private int[] root;
    private int[] rank; // rank attribute

    public QuickUnion(int size) {
        root = new int[size];
        rank = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
            rank[i] = 1; // initial the rank as 1
        }
    }
    // Path Compression
    public int find(int x) {
        if (root[x] == x) {
            return x;
        }
        // Recursively updating each traversed node
        return root[x] = find(root[x]); 
    }
    // Union by Rank
    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            // choose the root with larger rank as parent
            if (rank[rootX] > rank[rootY]) { 
                root[rootY] = rootX;
            } 
            // choose the root with larger rank as parent
            else if (rank[rootX] < rank[rootY]) { 
                root[rootX] = rootY;
            } 
            // if same rank
            else { 
                root[rootY] = rootX; // choose x as parent by default
                rank[rootX] += 1; // increasing the rank of x by 1
            }
        }
    }

    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }
}

Problem:
After path compression, every node below the root will become the direct child of the root, which makes the actual rank value differ from the one store in rank array. It will make the Union By Rank inaccurate. The solution may be (a) using just one optimization in implementation, or (b) using the number of node to replace height of the node for the Rank attribute.

Last updated on 2022-03-31

References

Graph - Explore - LeetCode

写在最后

Disjoint Set 和 Graph 相关的知识会继续学习，继续更新.
最后，希望大家一起交流，分享，指出问题，谢谢！

原创文章，转载请标明出处
Made by Mike_Zhang




感谢你的支持
Data Structure and Algorithm > Data Structure > Disjoint Set
#Java #数据结构 #Graph #Disjoint-Set
Disjoint Set Introduction - 并查集简介
https://ultrafish.io/post/disjoint-set-introduction/
Author
Mike_Zhang
Posted on
March 25, 2022
Licensed under